Примерная программа вступительных испытаний по математике

Содержание экзаменационной работы определяется на основе Федерального компонента государственного стандарта основного общего и среднего (полного) общего образования (приказ Минобразования России от 05.03.2004 № 1089 «Об утверждении федерального компонента государственных стандартов начального общего, основного общего и среднего (полного) общего образования»).

1. АЛГЕБРА
1. Корни и степени.
1. Корень степени n>1 и его свойства.
2. Степень с рациональным показателем и ее свойства.
3. Свойства степени с действительным показателем.
2. Логарифм.
1. Логарифм числа.
2. Логарифм произведения, частного, степени.
3. Десятичный и натуральный логарифмы, число е.
4. Преобразования простейших выражений, включающих арифметические операции, а также операцию возведения в степень и операцию логарифмирования.
3. Основы тригонометрии.
1. Синус, косинус, тангенс, котангенс произвольного угла.
2. Радианная мера угла.
3. Синус, косинус, тангенс и котангенс числа.
4. Основные тригонометрические тождества.
5. Формулы приведения.
6. Синус, косинус и тангенс суммы и разности двух углов.
7. Синус и косинус двойного угла.
8. Формулы половинного угла.
9. Преобразования суммы тригонометрических функций в произведение и произведения в сумму.
10. Выражение тригонометрических функций через тангенс половинного аргумента.
11. Преобразования простейших тригонометрических выражений.
12. Простейшие тригонометрические уравнения.
13. Решения тригонометрических уравнений.
14. Простейшие тригонометрические неравенства.
15. Арксинус, арккосинус, арктангенс числа.
4. ФУНКЦИИ
1. Функции. Область определения и множество значений.
2. График функции.
3. Построение графиков функций, заданных различными способами.
4. Свойства функций: монотонность, четность и нечетность, периодичность, ограниченность.
5. Промежутки возрастания и убывания, наибольшее и наименьшее значения, точки экстремума (локального максимума и минимума).
6. Графическая интерпретация. Примеры функциональных зависимостей в реальных процессах и явлениях.
7. Обратная функция. Область определения и область значений обратной функции. График обратной функции.
8. Степенная функция с натуральным показателем, ее свойства и график.
9. Тригонометрические функции, их свойства и графики; периодичность, основной период.
10. Показательная функция (экспонента), ее свойства и график.
11. Логарифмическая функция, ее свойства и график.
12. Преобразования графиков: параллельный перенос, симметрия относительно осей координат.
5. НАЧАЛА МАТЕМАТИЧЕСКОГО АНАЛИЗА
1. Понятие о пределе последовательности. Существование предела монотонной ограниченной последовательности.
2. Длина окружности и площадь круга как пределы последовательностей. Бесконечно убывающая геометрическая прогрессия и ее сумма.
3. Понятие о непрерывности функции.
4. Понятие о производной функции, физический и геометрический смысл производной. Уравнение касательной к графику функции.
5. Производные суммы, разности, произведения, частного.
6. Производные основных элементарных функций.
7. Применение производной к исследованию функций и построению графиков.
8. Понятие об определенном интеграле как площади криволинейной трапеции.
9. Первообразная. Формула Ньютона-Лейбница.
10. Примеры использования производной для нахождения наилучшего решения в прикладных, в том числе социально-экономических, задачах.
11. Нахождение скорости для процесса, заданного формулой или графиком.
12. Примеры применения интеграла в физике и геометрии. Вторая производная и ее физический смысл.
6. УРАВНЕНИЯ И НЕРАВЕНСТВА
1. Решение рациональных, показательных, логарифмических уравнений и неравенств. Решение иррациональных уравнений.
2. Основные приемы решения систем уравнений: подстановка, алгебраическое сложение, введение новых переменных.
3. Равносильность уравнений, неравенств, систем.
4. Решение простейших систем уравнений с двумя неизвестными.
5. Решение систем неравенств с одной переменной.
6. Использование свойств и графиков функций при решении уравнений и неравенств.
7. Метод интервалов. Изображение на координатной плоскости множества решений уравнений и неравенств с двумя переменными и их систем.
8. Применение математических методов для решения содержательных задач из различных областей науки и практики. Интерпретация результата, учет реальных ограничений.
2. ЭЛЕМЕНТЫ КОМБИНАТОРИКИ, СТАТИСТИКИ И ТЕОРИИ ВЕРОЯТНОСТЕЙ
1. Табличное и графическое представление данных.
2. Поочередный и одновременный выбор нескольких элементов из конечного множества.
3. Формулы числа перестановок, сочетаний, размещений.
4. Решение комбинаторных задач.
5. Формула бинома Ньютона.
6. Свойства биномиальных коэффициентов.
7. Треугольник Паскаля.
8. Элементарные и сложные события.
9. Рассмотрение случаев и вероятность суммы несовместных событий, вероятность противоположного события. Понятие о независимости событий. Вероятность и статистическая частота наступления события.
10. Решение практических задач с применением вероятностных методов.
3. ГЕОМЕТРИЯ
1. Прямые и плоскости в пространстве. Основные понятия стереометрии (точка, прямая, плоскость, пространство).
1. Пересекающиеся, параллельные и скрещивающиеся прямые.
2. Угол между прямыми в пространстве.
3. Перпендикулярность прямых.
4. Параллельность и перпендикулярность прямой и плоскости, признаки и свойства. Теорема о трех перпендикулярах. Перпендикуляр и наклонная. Угол между прямой и плоскостью.
5. Параллельность плоскостей, перпендикулярность плоскостей, признаки и свойства.
6. Расстояния от точки до плоскости.
7. Расстояние от прямой до плоскости.
8. Расстояние между параллельными плоскостями.
9. Параллельное проектирование. Изображение пространственных фигур.
2. Многогранники.
1. Вершины, ребра, грани многогранника.
2. Призма, ее основания, боковые ребра, высота, боковая поверхность. Прямая и наклонная призма. Правильная призма. Параллелепипед. Куб.
3. Пирамида, ее основание, боковые ребра, высота, боковая поверхность.
4. Треугольная пирамида.
5. Правильная пирамида.
6. Симметрии в кубе, в параллелепипеде.
7. Сечения куба, призмы, пирамиды.
8. Представление о правильных многогранниках (тетраэдр, куб, октаэдр, додекаэдр и икосаэдр).
3. Тела и поверхности вращения.
1. Цилиндр и конус.
2. Основание, высота, боковая поверхность, образующая, развертка.
3. Шар и сфера, их сечения, касательная плоскость к сфере.
4. Объемы тел и площади их поверхностей.
1. Формулы объема куба, прямоугольного параллелепипеда, призмы, цилиндра. Формулы объема пирамиды и конуса.
2. Формулы площади поверхностей цилиндра и конуса.
3. Формулы объема шара и площади сферы.
5. Координаты и векторы.
1. Декартовы координаты в пространстве.
2. Формула расстояния между двумя точками.
3. Уравнения сферы.
6. Векторы.
1. Модуль вектора.
2. Равенство векторов.
3. Сложение векторов и умножение вектора на число.
4. Угол между векторами.
5. Координаты вектора.
6. Скалярное произведение векторов.
7. Коллинеарные векторы.
8. Разложение вектора по двум неколлинеарным векторам.
9. Компланарные векторы.
10. Разложение по трем некомпланарным вектор

Примеры заданий с решениями.

Простейшие текстовые задачи

Вычисления

Аня ку­пи­ла про­езд­ной билет на месяц и сде­ла­ла за месяц 41 по­езд­ку. Сколь­ко руб­лей она сэко­но­ми­ла, если про­езд­ной билет стоит 580 руб­лей, а ра­зо­вая по­езд­ка — 20 руб­лей?

Ре­ше­ние.
Най­дем, что 41 по­езд­ка сто­и­ла бы 20×41 = 820 руб­лей. Зна­чит, Аня сэко­но­ми­ла 820 − 580 = 240 руб­лей.

Ответ: 240.

Округление с недостатком

По та­риф­но­му плану «Про­сто как день» ком­па­ния со­то­вой связи каж­дый вечер сни­ма­ет со счёта або­нен­та 16 руб­лей. Если на счету оста­лось мень­ше 16 руб­лей, то на сле­ду­ю­щее утро номер бло­ки­ру­ют до по­пол­не­ния счёта. Се­год­ня утром у Лизы на счету было 700 руб­лей. Сколь­ко дней (вклю­чая се­го­дняш­ний) она смо­жет поль­зо­вать­ся те­ле­фо­ном, не по­пол­няя счёт?
Ре­ше­ние.
За­ме­тим, что по­это­му Лизе хва­тит денег на 43 дня.
 Ответ: 43.

Округление с избытком

Боль­но­му про­пи­са­но ле­кар­ство, ко­то­рое нужно пить по 0,5 г 3 раза в день в те­че­ние 21 дня. В одной упа­ков­ке 10 таб­ле­ток ле­кар­ства по 0,5 г. Ка­ко­го наи­мень­ше­го ко­ли­че­ства упа­ко­вок хва­тит на весь курс ле­че­ния?

Ре­ше­ние.
Боль­но­му нужно вы­пить 0,5 · 3 · 21 = 31,5 г ле­кар­ства. В одной упа­ков­ке со­дер­жит­ся 0,5 · 10 = 5 г ле­кар­ства. Раз­де­лим 31,5 на 5:
.

Зна­чит, на курс ле­че­ния не­об­хо­ди­мо 7 упа­ко­вок.

Ответ: 7.

Проценты

Же­лез­но­до­рож­ный билет для взрос­ло­го стоит 720 руб­лей. Сто­и­мость би­ле­та для школь­ни­ка со­став­ля­ет 50% от сто­и­мо­сти би­ле­та для взрос­ло­го. Груп­па со­сто­ит из 15 школь­ни­ков и 2 взрос­лых. Сколь­ко руб­лей стоят би­ле­ты на всю груп­пу?
Ре­ше­ние.
Билет для ре­бен­ка стоит 720 · 0,5 = 360 руб. Сто­и­мость би­ле­тов на 15 школь­ни­ков и двух взрос­лых со­став­ля­ет 360 · 15 + 720 · 2 = 5400 + 1440 = 6840 руб.
 Ответ: 6840.

Проценты и округление

Фла­кон шам­пу­ня стоит 160 руб­лей. Какое наи­боль­шее число фла­ко­нов можно ку­пить на 1000 руб­лей во время рас­про­да­жи, когда скид­ка со­став­ля­ет 25% ?
Ре­ше­ние.
Во время рас­про­да­жи шам­пунь ста­нет сто­ить 160 − 0,25 ×160 = 120 руб­лей. Раз­де­лим 1000 на 120:

.
Зна­чит, можно будет ку­пить 8 фла­ко­нов шам­пу­ня.
Ответ: 8.

Чтение графиков и диаграмм

Определение величины по графику

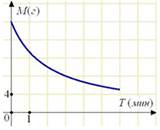
На гра­фи­ке изоб­ра­же­на за­ви­си­мость кру­тя­ще­го мо­мен­та ав­то­мо­биль­но­го дви­га­те­ля от числа его обо­ро­тов в ми­ну­ту. На оси абс­цисс от­кла­ды­ва­ет­ся число обо­ро­тов в ми­ну­ту. На оси ор­ди­нат — кру­тя­щий мо­мент в Н ×м. Чтобы ав­то­мо­биль начал дви­же­ние, кру­тя­щий мо­мент дол­жен быть не менее 60 Н × м. Какое наи­мень­шее число обо­ро­тов дви­га­те­ля в ми­ну­ту до­ста­точ­но, чтобы ав­то­мо­биль начал дви­же­ние?

Ре­ше­ние.
Из гра­фи­ка видно, что кру­тя­щий мо­мент 60 Н×м до­сти­га­ет­ся при 2000 обо­ро­тов дви­га­те­ля в ми­ну­ту (см. ри­су­нок).

Ответ: 2000.

Определение величины по диаграмме

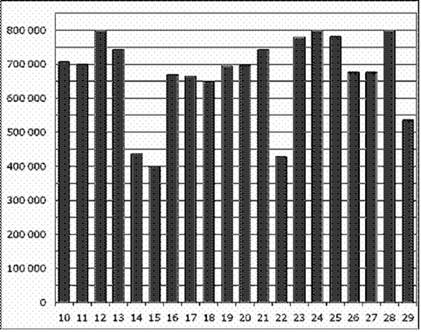
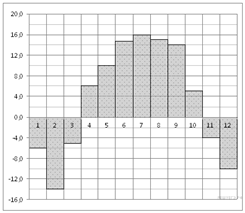
На диа­грам­ме по­ка­за­на сред­не­ме­сяч­ная тем­пе­ра­ту­ра в Ниж­нем Нов­го­ро­де (Горь­ком) за каж­дый месяц 1994 года. По го­ри­зон­та­ли ука­зы­ва­ют­ся ме­ся­цы, по вер­ти­ка­ли — тем­пе­ра­ту­ра в гра­ду­сах Цель­сия. Опре­де­ли­те по диа­грам­ме наи­мень­шую сред­не­ме­сяч­ную тем­пе­ра­ту­ру в 1994 году. Ответ дайте в гра­ду­сах Цель­сия.

Ре­ше­ние.
Из диа­грам­мы видно, что наи­мень­шая сред­не­ме­сяч­ная тем­пе­ра­ту­ра со­став­ля­ет −14 °C (см. ри­су­нок).

Ответ: −14.

Вычисление величин по графику или диаграмме

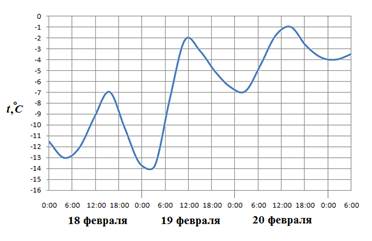
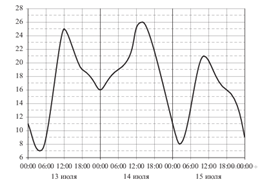
На ри­сун­ке по­ка­за­но из­ме­не­ние тем­пе­ра­ту­ры воз­ду­ха на про­тя­же­нии трех суток. По го­ри­зон­та­ли ука­зы­ва­ет­ся дата и время суток, по вер­ти­ка­ли — зна­че­ние тем­пе­ра­ту­ры в гра­ду­сах Цель­сия. Опре­де­ли­те по ри­сун­ку раз­ность между наи­боль­шей и наи­мень­шей тем­пе­ра­ту­рой воз­ду­ха 15 июля. Ответ дайте в гра­ду­сах Цель­сия.

Ре­ше­ние.
Из гра­фи­ка видно, что 15 июля наи­боль­шая тем­пе­ра­ту­ра со­став­ля­ла 21 °C, а наи­мень­шая 8 °C. Их раз­ность со­став­ля­ет 13 °C.
Ответ: 13.

Выбор оптимального варианта,

Выбор варианта из трех возможных

Ин­тер­нет-про­вай­дер (ком­па­ния, ока­зы­ва­ю­щая услу­ги по под­клю­че­нию к сети Ин­тер­нет) пред­ла­га­ет три та­риф­ных плана.

Поль­зо­ва­тель пред­по­ла­га­ет, что его тра­фик со­ста­вит 600 Мб в месяц и, ис­хо­дя из этого, вы­би­ра­ет наи­бо­лее де­ше­вый та­риф­ный план. Сколь­ко руб­лей за­пла­тит поль­зо­ва­тель за месяц, если его тра­фик дей­стви­тель­но будет равен 600 Мб?
Ре­ше­ние.
Рас­смот­рим все ва­ри­ан­ты.

По Плану «0» поль­зо­ва­тель по­тра­тит 2,5  600 = 1500 руб. в месяц за 600 Мб тра­фи­ка.

По плану «500» он по­тра­тит 550 руб. або­нент­ской платы за 500 Мб и 2  100 = 200 руб. сверх того. По­это­му пол­ная плата в месяц со­ста­вит 550 + 200 = 750 руб.

По плану «800» поль­зо­ва­тель по­тра­тит в месяц за 600 Мб тра­фи­ка 700 руб.

Наи­бо­лее вы­год­ный ва­ри­ант со­став­ля­ет 700 руб.

Ответ: 700.

Планиметрия: задачи, связанные с углами

Решение прямоугольного треугольника

В тре­уголь­ни­ке  угол  равен 90°, , . Най­ди­те .
Ре­ше­ние.
Имеем:

Ответ: 5.

Решение равнобедренного треугольника

В тре­уголь­ни­ке ABC AC = BC = 5,  Най­ди­те АВ.
Ре­ше­ние.
Тре­уголь­ник АВС рав­но­бед­рен­ный, по­это­му вы­со­та СН делит ос­но­ва­ние АВ по­по­лам. Тогда

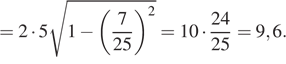
Ответ: 9,6.

 

Треугольники общего вида

Най­ди­те пло­щадь тре­уголь­ни­ка, две сто­ро­ны ко­то­ро­го равны 8 и 12, а угол между ними равен 30°.
Ре­ше­ние.
Пло­щадь тре­уголь­ни­ка равна по­ло­ви­не про­из­ве­де­ния его сто­рон на синус угла между ними. По­это­му

 см2.
Ответ: 24.

Параллелограммы

В па­рал­ле­ло­грам­ме ABCD AB = 3, AD = 21, . Най­ди­те боль­шую вы­со­ту па­рал­ле­ло­грам­ма.
Ре­ше­ние.
Боль­шая вы­со­та про­ве­де­на к мень­шей сто­ро­не. Имеем:

Ответ: 18.

Трапеция

Ос­но­ва­ния рав­но­бед­рен­ной тра­пе­ции равны 51 и 65. Бо­ко­вые сто­ро­ны равны 25. Най­ди­те синус остро­го угла тра­пе­ции.
Ре­ше­ние.
Пусть CE — вы­со­та
.
По тео­ре­ме Пи­фа­го­ра на­хо­дим: .
Тогда
.
Ответ: 0,96.

Чему равен ост­рый впи­сан­ный угол, опи­ра­ю­щий­ся на хорду, рав­ную ра­ди­у­су окруж­но­сти? Ответ дайте в гра­ду­сах.
Ре­ше­ние.

Рас­смот­рим тре­уголь­ник AOB. Он рав­но­сто­рон­ний, так как AO = OB = AB = R. По­это­му угол AOB = 60. Впи­сан­ный угол ACB равен по­ло­ви­не дуги, на ко­то­рую он опи­ра­ет­ся. Тем самым, он равен 30°.

 

Ответ: 30.

Касательная, хорда, секущая

Най­ди­те хорду, на ко­то­рую опи­ра­ет­ся угол 30°, впи­сан­ный в окруж­ность ра­ди­у­са 3.
Ре­ше­ние.

За­ме­тим, что . Зна­чит, , т. к. яв­ля­ет­ся цен­траль­ным углом, опи­ра­ю­щим­ся на ту же хорду. Со­от­вет­ствен­но, тре­уголь­ник AOB— рав­но­сто­рон­ний, так как AO = OB = AB = R = 3.

Ответ: 3.

Вписанные окружности

Пе­ри­метр тре­уголь­ни­ка равен 12, а ра­ди­ус впи­сан­ной окруж­но­сти равен 1. Най­ди­те пло­щадь этого тре­уголь­ни­ка.
Ре­ше­ние.
Пло­щадь тре­уголь­ни­ка равна про­из­ве­де­нию его по­лу­пе­ри­мет­ра на ра­ди­ус впи­сан­ной окруж­но­сти:

.

Ответ: 6.

Описанные окружности

Точки A, B, C, рас­по­ло­жен­ные на окруж­но­сти, делят ее на три дуги, гра­дус­ные ве­ли­чи­ны ко­то­рых от­но­сят­ся как 1 : 3 : 5. Най­ди­те боль­ший угол тре­уголь­ни­ка ABC. Ответ дайте в гра­ду­сах.
Ре­ше­ние.
Пусть мень­шая часть окруж­но­сти равна x, тогда

Боль­ший угол опи­ра­ет­ся на боль­шую дугу; впи­сан­ный угол равен по­ло­ви­не дуги, на ко­то­рую он опи­ра­ет­ся. Сле­до­ва­тель­но, ис­ко­мый угол равен по­ло­ви­не от 5 · 40° или 100°.

Ответ: 100.

Начала теории вероятностей

Классическое определение вероятности

1. На эк­за­мен вы­не­се­но 60 во­про­сов, Ан­дрей не вы­учил 3 из них. Най­ди­те ве­ро­ят­ность того, что ему по­па­дет­ся вы­учен­ный во­прос.
Ре­ше­ние.
Ан­дрей вы­учил 60 – 3 = 57 во­про­сов. По­это­му ве­ро­ят­ность того, что на эк­за­ме­не ему по­па­дет­ся вы­учен­ный во­прос равна

.
Ответ: 0,95.

2. В фирме такси в дан­ный мо­мент сво­бод­но 20 машин: 10 чер­ных, 2 жел­тых и 8 зе­ле­ных. По вы­зо­ву вы­еха­ла одна из машин, слу­чай­но ока­зав­ша­я­ся ближе всего к за­каз­чи­це. Най­ди­те ве­ро­ят­ность того, что к ней при­е­дет зе­ле­ное такси.
Ре­ше­ние.
Ве­ро­ят­ность того, что к за­каз­чи­це при­е­дет зе­ле­ное такси равна

.
Ответ: 0,4.
3. На та­рел­ке 16 пи­рож­ков: 7 с рыбой, 5 с ва­ре­ньем и 4 с виш­ней. Юля на­у­гад вы­би­ра­ет один пи­ро­жок. Най­ди­те ве­ро­ят­ность того, что он ока­жет­ся с виш­ней.
Ре­ше­ние.
ве­ро­ят­ность того, что пи­ро­жок ока­жет­ся с виш­ней равна

.
Ответ: 0,25.

Теоремы о вероятностях событий

1. Ве­ро­ят­ность того, что ба­та­рей­ка бра­ко­ван­ная, равна 0,06. По­ку­па­тель в ма­га­зи­не вы­би­ра­ет слу­чай­ную упа­ков­ку, в ко­то­рой две таких ба­та­рей­ки. Най­ди­те ве­ро­ят­ность того, что обе ба­та­рей­ки ока­жут­ся ис­прав­ны­ми.
Ре­ше­ние.
Ве­ро­ят­ность того, что ба­та­рей­ка ис­прав­на, равна 0,94. Ве­ро­ят­ность про­из­ве­де­ния не­за­ви­си­мых со­бы­тий (обе ба­та­рей­ки ока­жут­ся ис­прав­ны­ми) равна про­из­ве­де­нию ве­ро­ят­но­стей этих со­бы­тий: 0,94·0,94 = 0,8836.

Ответ: 0,8836.
2. Ка­ко­ва ве­ро­ят­ность того, что слу­чай­но вы­бран­ный те­ле­фон­ный номер окан­чи­ва­ет­ся двумя чётными циф­ра­ми?
Ре­ше­ние.
Ве­ро­ят­ность того, что на одном из тре­бу­е­мых мест ока­жет­ся чётное число равна 0,5. Сле­до­ва­тель­но, ве­ро­ят­ность того, что на двух ме­стах од­но­вре­мен­но ока­жут­ся два чётных числа равна 0,5 · 0,5=0,25.

Ответ: 0,25.

Простейшие уравнения

Линейные, квадратные, кубические уравнения

1. Най­ди­те ко­рень урав­не­ния: .

Ре­ше­ние.
По­сле­до­ва­тель­но по­лу­ча­ем:

Ответ: 13.
2. Най­ди­те ко­рень урав­не­ния: .
Ре­ше­ние.
По­сле­до­ва­тель­но по­лу­ча­ем:
.
Ответ: −5.
3. Най­ди­те ко­рень урав­не­ния:  Если урав­не­ние имеет более од­но­го корня, ука­жи­те мень­ший из них.
Ре­ше­ние.
Решим квад­рат­ное урав­не­ние:

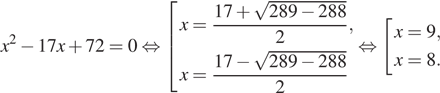
При­ме­ча­ние.
По тео­ре­ме, об­рат­ной тео­ре­ме Виета, сумма кор­ней урав­не­ния равна 17, а их про­из­ве­де­ние равно 72. Тем самым, это числа 8 и 9.

Ответ: 8.
4. Ре­ши­те урав­не­ние .
Ре­ше­ние.
Вы­пол­ним пре­об­ра­зо­ва­ния, ис­поль­зуя фор­му­лы :

Ответ: −1,5.
5. Ре­ши­те урав­не­ние .
Ре­ше­ние.
Ис­поль­зу­ем фор­му­лы квад­ра­та суммы и раз­но­сти:

Ответ: −6.

Рациональные уравнения

1. Най­ди­те ко­рень урав­не­ния: 
Ре­ше­ние.
Из­ба­вим­ся от зна­ме­на­те­ля:
.
Ответ: 14.

Иррациональные уравнения

1. Най­ди­те ко­рень урав­не­ния .
Ре­ше­ние.
Воз­ве­дем в квад­рат:

Ответ: 3.

Простейшие уравнения

 

Показательные уравнения

 Най­ди­те ко­рень урав­не­ния .
Ре­ше­ние.
Пе­рей­дем к од­но­му ос­но­ва­нию сте­пе­ни:

Ответ: −1.

Логарифмические уравнения

1. Най­ди­те ко­рень урав­не­ния .
Ре­ше­ние.
По­сле­до­ва­тель­но по­лу­ча­ем:

Ответ: −124.
2. Най­ди­те ко­рень урав­не­ния .
Ре­ше­ние.
По­сле­до­ва­тель­но по­лу­ча­ем:

Ответ: 21.

Тригонометрические уравнения

Най­ди­те корни урав­не­ния:  В ответ за­пи­ши­те наи­боль­ший от­ри­ца­тель­ный ко­рень.
Ре­ше­ние.
По­сле­до­ва­тель­но по­лу­ча­ем:

Зна­че­ни­ям  со­от­вет­ству­ют по­ло­жи­тель­ные корни.
Если , то  и .
Если , то  и .
Зна­че­ни­ям  со­от­вет­ству­ют мень­шие зна­че­ния кор­ней.
Сле­до­ва­тель­но, наи­боль­шим от­ри­ца­тель­ным кор­нем яв­ля­ет­ся число .

Ответ: −4.

 

Планиметрия: задачи, связанные с углами

Задачи на многоугольники и окружности

1. В па­рал­ле­ло­грам­ме ABCD вы­со­та, опу­щен­ная на сто­ро­ну AB, равна 4, AD = 8. Най­ди­те синус угла B.

Ре­ше­ние.
Имеем:

Ответ: 0,5.
2. Пло­щадь тре­уголь­ни­ка равна 24, а ра­ди­ус впи­сан­ной окруж­но­сти равен 2. Най­ди­те пе­ри­метр этого тре­уголь­ни­ка.
Ре­ше­ние.
Из фор­му­лы , где p — по­лу­пе­ри­метр, на­хо­дим, что пе­ри­метр опи­сан­но­го мно­го­уголь­ни­ка равен от­но­ше­нию удво­ен­ной пло­ща­ди к ра­ди­у­су впи­сан­ной окруж­но­сти:
.
Ответ: 24.

Применение тригонометрии.

1. В тре­уголь­ни­ке  угол  равен 90°, . Най­ди­те .

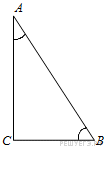
Ре­ше­ние.
Имеем:

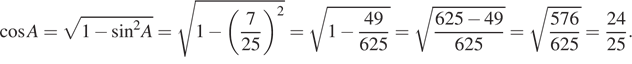
Ответ: 0,96.
2.  В тре­уголь­ни­ке  , , тан­генс внеш­не­го угла при вер­ши­не  равен . Най­ди­те .

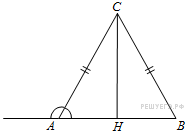
Ре­ше­ние.
так как


Ответ: 7.

Производная и первообразная

Физический смысл производной

Ма­те­ри­аль­ная точка дви­жет­ся пря­мо­ли­ней­но по за­ко­ну  (где x — рас­сто­я­ние от точки от­сче­та в мет­рах, t — время в се­кун­дах, из­ме­рен­ное с на­ча­ла дви­же­ния). Най­ди­те ее ско­рость (в м/с) в мо­мент вре­ме­ни t = 9 с.
Ре­ше­ние.
Най­дем закон из­ме­не­ния ско­ро­сти:
.
При t = 9 c имеем:

 

 м/с.

Ответ: 60.

Геометрический смысл производной, касательная

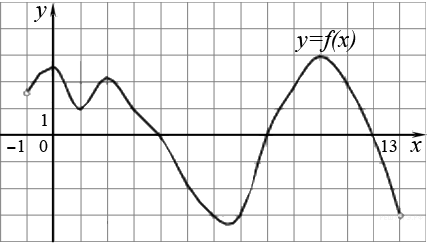
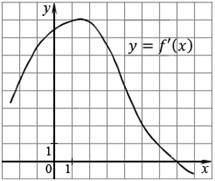
На ри­сун­ке изоб­ражён гра­фик функ­ции y=f(x) и ка­са­тель­ная к нему в точке с абс­цис­сой x0. Най­ди­те зна­че­ние про­из­вод­ной функ­ции f(x) в точке x0.

Ре­ше­ние.
Зна­че­ние про­из­вод­ной в точке ка­са­ния равно уг­ло­во­му ко­эф­фи­ци­ен­ту ка­са­тель­ной, ко­то­рый в свою оче­редь равен тан­ген­су угла на­кло­на дан­ной ка­са­тель­ной к оси абс­цисс. По­стро­им тре­уголь­ник с вер­ши­на­ми в точ­ках A (1; 2), B (1; −4), C(−2; −4). Угол на­кло­на ка­са­тель­ной к оси абс­цисс будет равен углу ACB:

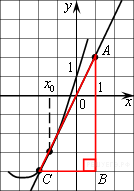
Ответ: 2.

Применение производной к исследованию функций

На ри­сун­ке изоб­ра­жен гра­фик про­из­вод­ной функ­ции , опре­де­лен­ной на ин­тер­ва­ле . Най­ди­те про­ме­жут­ки воз­рас­та­ния функ­ции . В от­ве­те ука­жи­те сумму целых точек, вхо­дя­щих в эти про­ме­жут­ки.

Ре­ше­ние.
Про­ме­жут­ки воз­рас­та­ния дан­ной функ­ции f(x) со­от­вет­ству­ют про­ме­жут­кам, на ко­то­рых ее про­из­вод­ная не­от­ри­ца­тель­на, то есть про­ме­жут­кам (−6; −5,2] и [2; 6). Дан­ные про­ме­жут­ки со­дер­жат целые точки 2, 3, 4 и 5. Их сумма равна 14.

Ответ: 14.

Первообразная

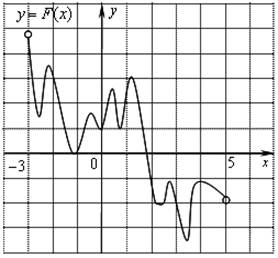
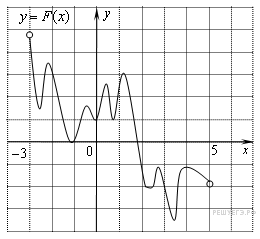
 На ри­сун­ке изоб­ражён гра­фик функ­ции y = F(x) — одной из пер­во­об­раз­ных функ­ции f(x), опре­делённой на ин­тер­ва­ле (−3; 5). Най­ди­те ко­ли­че­ство ре­ше­ний урав­не­ния f(x)=0 на от­рез­ке [−2; 4].

Ре­ше­ние.
По опре­де­ле­нию пер­во­об­раз­ной на ин­тер­ва­ле (−3; 5) спра­вед­ли­во ра­вен­ство

Сле­до­ва­тель­но, ре­ше­ни­я­ми урав­не­ния f(x)=0 яв­ля­ют­ся точки экс­тре­му­мов изоб­ра­жен­ной на ри­сун­ке функ­ции F(x) Это точки −2,6; −2,2; −1,2; −0,5; 0; 0,4; 0,8; 1,2; 2,2; 2,8; 3,4; 3,8. Из них на от­рез­ке [−2;4] лежат 10 точек. Таким об­ра­зом, на от­рез­ке [−2;4] урав­не­ние  имеет 10 ре­ше­ний.

Ответ: 10.

Вычисления и преобразования

Преобразования числовых рациональных выражений

Най­ди­те зна­че­ние вы­ра­же­ния .
Ре­ше­ние.
Вы­пол­ним пре­об­ра­зо­ва­ния:

.
Ответ: 80,625.

Преобразования алгебраических выражений и дробей

Най­ди­те зна­че­ние вы­ра­же­ния .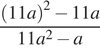
Ре­ше­ние.
Вы­пол­ним пре­об­ра­зо­ва­ния:
.
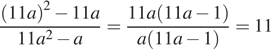Ответ: 11.

Ответ: 2.

Вычисления и преобразования

Преобразования числовых иррациональных выражений

Най­ди­те зна­че­ние вы­ра­же­ния .
Ре­ше­ние.
Вы­пол­ним пре­об­ра­зо­ва­ния:

Ответ: 33.

Преобразования буквенных иррациональных выражений

Най­ди­те зна­че­ние вы­ра­же­ния  при .
Ре­ше­ние.
Вы­пол­ним пре­об­ра­зо­ва­ния:
.
Ответ: 5.

Вычисление значений степенных выражений

Най­ди­те зна­че­ние вы­ра­же­ния .
Ре­ше­ние.
Вы­пол­ним пре­об­ра­зо­ва­ния:
.
Ответ: 5.

Действия со степенями

Най­ди­те зна­че­ние вы­ра­же­ния .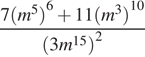
Ре­ше­ние.
Ис­поль­зу­ем свой­ства сте­пе­ней:
.

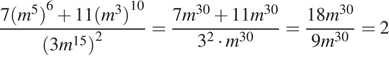Вычисления и преобразования

Вычисление значений тригонометрических выражений

Най­ди­те , если  и .
Ре­ше­ние.
По­сколь­ку угол альфа лежит в четвёртой чет­вер­ти, его тан­генс от­ри­ца­те­лен. По­это­му
.
Ответ: -3.

Преобразования числовых тригонометрических выражений

Най­ди­те зна­че­ние вы­ра­же­ния .
Ре­ше­ние.
Ис­поль­зу­ем фор­му­лу си­ну­са двой­но­го угла  :

.
Ответ: 6.

Преобразования буквенных тригонометрических выражений

Най­ди­те зна­че­ние вы­ра­же­ния .
Ре­ше­ние.
В силу пе­ри­о­дич­но­сти ко­си­ну­са . Далее ис­поль­зу­ем фор­му­лы при­ве­де­ния:
.
Ответ: 2.

Преобразования числовых логарифмических выражений

 Най­ди­те зна­че­ние вы­ра­же­ния .
Ре­ше­ние.
Вы­пол­ним пре­об­ра­зо­ва­ния:
.
Ответ: 8.

Преобразования буквенных логарифмических выражений

Най­ди­те зна­че­ние вы­ра­же­ния , если .
Ре­ше­ние.
Вы­пол­ним пре­об­ра­зо­ва­ния:
.
Ответ: 22.

Задачи с прикладным содержанием

Линейные уравнения и неравенства

При тем­пе­ра­ту­ре  рельс имеет длину  м. При воз­рас­та­нии тем­пе­ра­ту­ры про­ис­хо­дит теп­ло­вое рас­ши­ре­ние рель­са, и его длина, вы­ра­жен­ная в мет­рах, ме­ня­ет­ся по за­ко­ну , где  — ко­эф­фи­ци­ент теп­ло­во­го рас­ши­ре­ния,  — тем­пе­ра­ту­ра (в гра­ду­сах Цель­сия). При какой тем­пе­ра­ту­ре рельс удли­нит­ся на 3 мм? Ответ вы­ра­зи­те в гра­ду­сах Цель­сия.
Ре­ше­ние.
За­да­ча сво­дит­ся к ре­ше­нию урав­не­ния  мм при за­дан­ных зна­че­ни­ях длины  м и ко­эф­фи­ци­ен­та теп­ло­во­го рас­ши­ре­ния :

.
Ответ: 25.

Квадратные и степенные уравнения и неравенства

После дождя уро­вень воды в ко­лод­це может по­вы­сить­ся. Маль­чик из­ме­ря­ет время  па­де­ния не­боль­ших ка­меш­ков в ко­ло­дец и рас­счи­ты­ва­ет рас­сто­я­ние до воды по фор­му­ле , где  – рас­сто­я­ние в мет­рах,  – время па­де­ния в се­кун­дах. До дождя время па­де­ния ка­меш­ков со­став­ля­ло 0,6 с. На сколь­ко дол­жен под­нять­ся уро­вень воды после дождя, чтобы из­ме­ря­е­мое время из­ме­ни­лось на 0,2 с? Ответ вы­ра­зи­те в мет­рах.
Ре­ше­ние.
Пусть  – рас­сто­я­ние до воды до дождя,  – рас­сто­я­ние до воды после дождя. После дождя уро­вень воды в ко­лод­це по­вы­сит­ся, рас­сто­я­ние до воды умень­шит­ся, и время па­де­ния умень­шит­ся, ста­нет рав­ным  с. Уро­вень воды под­ни­мет­ся на  мет­ров.

Ответ: 1.

Рациональные уравнения и неравенства

Для по­лу­че­ния на экра­не уве­ли­чен­но­го изоб­ра­же­ния лам­поч­ки в ла­бо­ра­то­рии ис­поль­зу­ет­ся со­би­ра­ю­щая линза с глав­ным фо­кус­ным рас­сто­я­ни­ем  см. Рас­сто­я­ние  от линзы до лам­поч­ки может из­ме­нять­ся в пре­де­лах от 30 до 50 см, а рас­сто­я­ние  от линзы до экра­на – в пре­де­лах от 150 до 180 см. Изоб­ра­же­ние на экра­не будет чет­ким, если вы­пол­не­но со­от­но­ше­ние . Ука­жи­те, на каком наи­мень­шем рас­сто­я­нии от линзы можно по­ме­стить лам­поч­ку, чтобы еe изоб­ра­же­ние на экра­не было чeтким. Ответ вы­ра­зи­те в сан­ти­мет­рах.
Ре­ше­ние.
По­сколь­ку  имеем:

Наи­мень­ше­му воз­мож­но­му  зна­че­нию со­от­вет­ству­ет наи­боль­шее зна­че­ние левой части по­лу­чен­но­го ра­вен­ства, и, со­от­вет­ствен­но, наи­боль­шее воз­мож­ное зна­че­ние пра­вой части ра­вен­ства. Раз­ность  в пра­вой части ра­вен­ства до­сти­га­ет наи­боль­ше­го зна­че­ния при наи­мень­шем зна­че­нии вы­чи­та­е­мо­го , ко­то­рое до­сти­га­ет­ся при наи­боль­шем воз­мож­ном зна­че­нии зна­ме­на­те­ля . По­это­му , от­ку­да

 см.

По усло­вию лам­поч­ка долж­на на­хо­дить­ся на рас­сто­я­нии от 30 до 50 см от линзы. Най­ден­ное зна­че­ние удо­вле­тво­ря­ет усло­вию.

Ответ: 36.

Иррациональные уравнения и неравенства

Ав­то­мо­биль раз­го­ня­ет­ся на пря­мо­ли­ней­ном участ­ке шоссе с по­сто­ян­ным уско­ре­ни­ем  км/ч 2 . Ско­рость вы­чис­ля­ет­ся по фор­му­ле  , где  — прой­ден­ный ав­то­мо­би­лем путь. Най­ди­те уско­ре­ние, с ко­то­рым дол­жен дви­гать­ся ав­то­мо­биль, чтобы, про­ехав один ки­ло­метр, при­об­ре­сти ско­рость 100 км/ч. Ответ вы­ра­зи­те в км/ч2 .
Ре­ше­ние.
Найдём, при каком уско­ре­нии гон­щик до­стиг­нет тре­бу­е­мой ско­ро­сти, про­ехав один ки­ло­метр. За­да­ча сво­дит­ся к ре­ше­нию урав­не­ния  при из­вест­ном зна­че­нии длины пути  км:

 км/ч2.

Если его уско­ре­ние будет пре­вос­хо­дить най­ден­ное, то, про­ехав один ки­ло­метр, гон­щик наберёт боль­шую ско­рость, по­это­му наи­мень­шее не­об­хо­ди­мое уско­ре­ние равно 5000 км/ч2.

Ответ: 5000.

Показательные уравнения и неравенства

При адиа­ба­ти­че­ском про­цес­се для иде­аль­но­го газа вы­пол­ня­ет­ся закон  Пам5, где – дав­ле­ние в газе в пас­ка­лях,  – объeм газа в ку­би­че­ских мет­рах, . Най­ди­те, какой объём  (в куб. м) будет за­ни­мать газ при дав­ле­нии , рав­ном  Па.
Ре­ше­ние.
По­сколь­ку про­из­ве­де­ние дав­ле­ния на сте­пень объёма по­сто­ян­но, а дав­ле­ние не ниже , при за­дан­ных зна­че­ни­ях па­ра­мет­ров  и  Пам5 имеем не­ра­вен­ство:

.
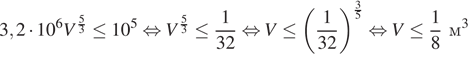Ответ: 0,125.

Логарифмические уравнения и неравенства

В те­ле­ви­зо­ре ёмкость вы­со­ко­вольт­но­го кон­ден­са­то­ра в те­ле­ви­зо­ре  Ф. Па­рал­лель­но с кон­ден­са­то­ром под­ключeн ре­зи­стор с со­про­тив­ле­ни­ем  Ом. Во время ра­бо­ты те­ле­ви­зо­ра на­пря­же­ние на кон­ден­са­то­ре  кВ. После вы­клю­че­ния те­ле­ви­зо­ра на­пря­же­ние на кон­ден­са­то­ре убы­ва­ет до зна­че­ния U (кВ) за время, опре­де­ля­е­мое вы­ра­же­ни­ем  (с), где  – по­сто­ян­ная. Опре­де­ли­те на­пря­же­ние на кон­ден­са­то­ре, если после вы­клю­че­ния те­ле­ви­зо­ра про­шло 21 с. Ответ дайте в ки­ло­воль­тах.
Ре­ше­ние.
За­да­ча сво­дит­ся к ре­ше­нию не­ра­вен­ства  при за­дан­ных зна­че­ни­ях на­чаль­но­го на­пря­же­ния на кон­ден­са­то­ре  кВ, со­про­тив­ле­ния ре­зи­сто­ра  Ом и ёмко­сти кон­ден­са­то­ра  Ф:

 кВ.
Ответ: 2.

Тригонометрические уравнения и неравенства

Мяч бро­си­ли под углом  к плос­кой го­ри­зон­таль­ной по­верх­но­сти земли. Время полeта мяча (в се­кун­дах) опре­де­ля­ет­ся по фор­му­ле . При каком зна­че­нии угла  (в гра­ду­сах) время полeта со­ста­вит 3 се­кун­ды, если мяч бро­са­ют с на­чаль­ной ско­ро­стью  м/с? Счи­тай­те, что уско­ре­ние сво­бод­но­го па­де­ния  м/с.
Ре­ше­ние.
За­да­ча сво­дит­ся к ре­ше­нию не­ра­вен­ства  на ин­тер­ва­ле  при за­дан­ных зна­че­ни­ях на­чаль­ной ско­ро­сти и уско­ре­ния сво­бод­но­го па­де­ния:

.
Ответ: 30.

Текстовые задачи

Задачи на проценты, сплавы и смеси

В 2008 году в го­род­ском квар­та­ле про­жи­ва­ло  че­ло­век. В 2009 году, в ре­зуль­та­те стро­и­тель­ства новых домов, число жи­те­лей вы­рос­ло на , а в 2010 году на  по срав­не­нию с 2009 годом. Сколь­ко че­ло­век стало про­жи­вать в квар­та­ле в 2010 году?
Ре­ше­ние.
В 2009 году число жи­те­лей стало  че­ло­век, а в 2010 году число жи­те­лей стало  че­ло­век.

Ответ: 47 088.

Задачи на движение по прямой

Из пунк­та A в пункт B од­но­вре­мен­но вы­еха­ли два ав­то­мо­би­ля. Пер­вый про­ехал с по­сто­ян­ной ско­ро­стью весь путь. Вто­рой про­ехал первую по­ло­ви­ну пути со ско­ро­стью 24 км/ч, а вто­рую по­ло­ви­ну пути – со ско­ро­стью, на 16 км/ч боль­шей ско­ро­сти пер­во­го, в ре­зуль­та­те чего при­был в пункт B од­но­вре­мен­но с пер­вым ав­то­мо­би­лем. Най­ди­те ско­рость пер­во­го ав­то­мо­би­ля. Ответ дайте в км/ч.
Ре­ше­ние.
Пусть  км/ч — ско­рость пер­во­го ав­то­мо­би­ля, тогда ско­рость вто­ро­го ав­то­мо­би­ля на вто­рой по­ло­ви­не пути равна  км/ч. При­мем рас­сто­я­ние между пунк­та­ми за 1. Ав­то­мо­би­ли были в пути одно и то же время, от­сю­да имеем:

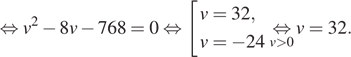
Таким об­ра­зом, ско­рость пер­во­го ав­то­мо­би­ля была равна 32 км/ч.

Ответ: 32.

Задачи на движение по окружности

Два мо­то­цик­ли­ста стар­ту­ют од­но­вре­мен­но в одном на­прав­ле­нии из двух диа­мет­раль­но про­ти­во­по­лож­ных точек кру­го­вой трас­сы, длина ко­то­рой равна 14 км. Через сколь­ко минут мо­то­цик­ли­сты по­рав­ня­ют­ся в пер­вый раз, если ско­рость од­но­го из них на 21 км/ч боль­ше ско­ро­сти дру­го­го?
Ре­ше­ние.
Пусть v км/ч — ско­рость пер­во­го мо­то­цик­ли­ста, тогда ско­рость вто­ро­го мо­то­цик­ли­ста равна v + 21 км/ч. Пусть пер­вый раз мо­то­цик­ли­сты по­рав­ня­ют­ся через  часов. Для того, чтобы мо­то­цик­ли­сты по­рав­ня­лись, более быст­рый дол­жен пре­одо­леть из­на­чаль­но раз­де­ля­ю­щее их рас­сто­я­ние, рав­ное по­ло­ви­не длины трас­сы. По­это­му

.
Таким об­ра­зом, мо­то­цик­ли­сты по­рав­ня­ют­ся через  часа или через 20 минут.

Ответ: 20.

Задачи на движение по воде

Мо­тор­ная лодка про­шла про­тив те­че­ния реки 112 км и вер­ну­лась в пункт от­прав­ле­ния, за­тра­тив на об­рат­ный путь на 6 часов мень­ше. Най­ди­те ско­рость те­че­ния, если ско­рость лодки в не­по­движ­ной воде равна 11 км/ч. Ответ дайте в км/ч.
Ре­ше­ние.
Пусть  км/ч – ско­рость те­че­ния реки, тогда ско­рость лодки по те­че­нию равна  км/ч, а ско­рость лодки про­тив те­че­ния равна  км/ч. На об­рат­ный путь лодка за­тра­ти­ла на 6 часов мень­ше, от­сю­да имеем:

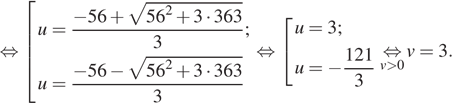
Таким об­ра­зом, ско­рость те­че­ния реки равна 3 км/ч.

Ответ: 3.

Задачи на совместную работу

 Заказ на из­го­тов­ле­ние 110 де­та­лей пер­вый ра­бо­чий вы­пол­ня­ет на 1 час быст­рее, чем вто­рой. Сколь­ко де­та­лей за час из­го­тав­ли­ва­ет вто­рой ра­бо­чий, если из­вест­но, что пер-вый за час из­го­тав­ли­ва­ет на 1 де­таль боль­ше?
Ре­ше­ние.
Обо­зна­чим  — число де­та­лей, ко­то­рые из­го­тав­ли­ва­ет за час вто­рой ра­бо­чий. Тогда пер­вый ра­бо­чий за час из­го­тав­ли­ва­ет  де­таль. На из­го­тов­ле­ние 110 де­та­лей пер­вый ра­бо­чий тра­тит на 1 час мень­ше, чем вто­рой ра­бо­чий, от­сю­да имеем:

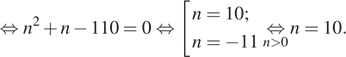
Таким об­ра­зом, вто­рой ра­бо­чий из­го­тав­ли­ва­ет 10 де­та­лей в час.

 

Ответ: 10.

Задачи на прогрессии

Бри­га­да ма­ля­ров кра­сит забор дли­ной 240 мет­ров, еже­днев­но уве­ли­чи­вая норму по­крас­ки на одно и то же число мет­ров. Из­вест­но, что за пер­вый и по­след­ний день в сумме бри­га­да по­кра­си­ла 60 мет­ров за­бо­ра. Опре­де­ли­те, сколь­ко дней бри­га­да ма­ля­ров кра­си­ла весь забор.
Ре­ше­ние.
Пусть бри­га­да в пер­вый день бри­га­да по­кра­си­ла  мет­ров за­бо­ра, во вто­рой — , … , в по­след­ний —  мет­ров за­бо­ра. Тогда  м, а за  дней было по­кра­ше­но

 мет­ров за­бо­ра.

По­сколь­ку всего было по­кра­ше­но 240 мет­ров за­бо­ра, имеем: . Таким об­ра­зом, бри­га­да кра­си­ла забор в те­че­ние 8 дней.

Ответ: 8.

 

Наибольшее и наименьшее значение функций

Исследование степенных и иррациональных функций

Най­ди­те точку мак­си­му­ма функ­ции .
Ре­ше­ние.
Най­дем про­из­вод­ную за­дан­ной функ­ции:

Най­дем нули про­из­вод­ной:

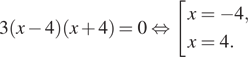
Опре­де­лим знаки про­из­вод­ной функ­ции и изоб­ра­зим на ри­сун­ке по­ве­де­ние функ­ции:

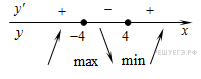
Ис­ко­мая точка мак­си­му­ма .

Ответ: −4.

Исследование частных

Най­ди­те точку мак­си­му­ма функ­ции 
Ре­ше­ние.
Най­дем про­из­вод­ную за­дан­ной функ­ции:

Най­дем нули про­из­вод­ной:

Опре­де­лим знаки про­из­вод­ной функ­ции и изоб­ра­зим на ри­сун­ке по­ве­де­ние функ­ции:

Ис­ко­мая точка мак­си­му­ма .

Ответ: 17.

Исследование произведений

Най­ди­те наи­мень­шее зна­че­ние функ­ции  на от­рез­ке .
Ре­ше­ние.
Най­дем про­из­вод­ную за­дан­ной функ­ции:

Най­дем нули про­из­вод­ной на за­дан­ном от­рез­ке:

Опре­де­лим знаки про­из­вод­ной функ­ции и изоб­ра­зим на ри­сун­ке по­ве­де­ние функ­ции:

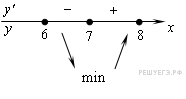
Наи­мень­шим зна­че­ни­ем за­дан­ной функ­ции на от­рез­ке  будет .

Ответ: −1.

Исследование тригонометрических функций

Най­ди­те наи­боль­шее зна­че­ние функ­ции  на от­рез­ке .
Ре­ше­ние.
Най­дем про­из­вод­ную за­дан­ной функ­ции:

Най­дем нули про­из­вод­ной на за­дан­ном от­рез­ке:

Опре­де­лим знаки про­из­вод­ной функ­ции на за­дан­ном от­рез­ке и изоб­ра­зим на ри­сун­ке по­ве­де­ние функ­ции:

В точке  за­дан­ная функ­ция имеет мак­си­мум, яв­ля­ю­щий­ся ее наи­боль­шим зна­че­ни­ем на за­дан­ном от­рез­ке. Най­дем это наи­боль­шее зна­че­ние:

.
Ответ: 12.

Исследование показательных и логарифмических функций

 Най­ди­те наи­мень­шее зна­че­ние функ­ции  на от­рез­ке [−2,5; 0].
Ре­ше­ние.
Най­дем про­из­вод­ную за­дан­ной функ­ции:

Най­дем нули про­из­вод­ной на за­дан­ном от­рез­ке:

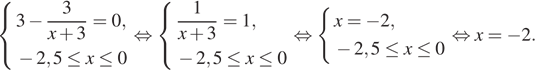
Опре­де­лим знаки про­из­вод­ной функ­ции на за­дан­ном от­рез­ке и изоб­ра­зим на ри­сун­ке по­ве­де­ние функ­ции:

В точке  за­дан­ная функ­ция имеет ми­ни­мум, яв­ля­ю­щий­ся ее наи­мень­шим зна­че­ни­ем на за­дан­ном от­рез­ке. Най­дем это наи­мень­шее зна­че­ние:

Ответ: −6.

Исследование функций без помощи производной

Най­ди­те точку мак­си­му­ма функ­ции .

Ре­ше­ние.
Квад­рат­ный трех­член  с от­ри­ца­тель­ным стар­шим ко­эф­фи­ци­ен­том до­сти­га­ет мак­си­му­ма в точке , в нашем слу­чае — в точке −2. По­сколь­ку функ­ция  воз­рас­та­ю­щая, а за­дан­ная функ­ция опре­де­ле­на при най­ден­ном зна­че­нии пе­ре­мен­ной, она до­сти­га­ет мак­си­му­ма в той же точке, в ко­то­рой до­сти­га­ет мак­си­му­ма под­ко­рен­ное вы­ра­же­ние.

Ответ: −2.

 

Уравнения

Логарифмические и показательные уравнения

а) Ре­ши­те урав­не­ние 
б) Най­ди­те все корни этого урав­не­ния, при­над­ле­жа­щие от­рез­ку 
Ре­ше­ние.
а) За­ме­тим, что урав­не­ние опре­де­ле­но при любом  За­пи­шем ис­ход­ное урав­не­ние в виде:

 

Зна­чит, либо  от­ку­да  или  либо , от­ку­да  или 
б) По­сколь­ку  от­рез­ку  при­над­ле­жат корни  и 
Ответ: а)  б) 

 

Тригонометрические уравнения

а) Ре­ши­те урав­не­ние 
б) Най­ди­те все корни этого урав­не­ния, при­над­ле­жа­щие от­рез­ку 
Ре­ше­ние.
а) Пре­об­ра­зу­ем урав­не­ние:

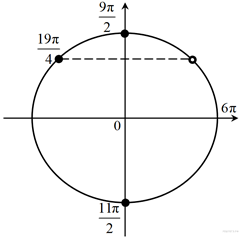
б) При по­мо­щи чис­ло­вой пря­мой или три­го­но­мет­ри­че­ской окруж­но­сти (см. рис.) для каж­дой из за­да­ю­щих ре­ше­ния серий от­бе­рем корни урав­не­ния, при­над­ле­жа­щие от­рез­ку 
На­хо­дим три ре­ше­ния: 

 

 

Ответ: а)  б) 

Тригонометрические уравнения, исследование ОДЗ

 а) Ре­ши­те урав­не­ние 
б) Най­ди­те все корни этого урав­не­ния, при­над­ле­жа­щие от­рез­ку 
Ре­ше­ние.

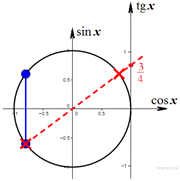
а) Дробь равна нулю, когда чис­ли­тель равен нулю, а зна­ме­на­тель от­ли­чен от нуля:

Из урав­не­ния  по­лу­ча­ем

 или 
Не­ра­вен­ству  удо­вле­тво­ря­ет толь­ко серия 

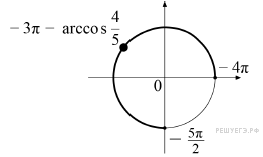
б) При по­мо­щи три­го­но­мет­ри­че­ской окруж­но­сти отберём корни урав­не­ния, ле­жа­щие на от­рез­ке По­лу­чим 
Ответ: а) ; б) 

Уравнения смешанного типа

 а) Ре­ши­те урав­не­ние 
б) Най­ди­те все корни этого урав­не­ния, при­над­ле­жа­щие от­рез­ку 
Ре­ше­ние.

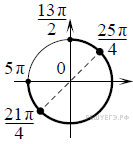
а) Пре­об­ра­зу­ем ис­ход­ное урав­не­ние:

б) С по­мо­щью чис­ло­вой окруж­но­сти от­бе­рем корни, при­над­ле­жа­щие от­рез­ку  По­лу­чим числа: 

Ответ: а)  б) 

 

Планиметрическая задача

Многоугольники и их свойства

На сто­ро­не CD квад­ра­та ABCD по­стро­ен рав­но­сто­рон­ний тре­уголь­ник CPD. Най­ди­те вы­со­ту тре­уголь­ни­ка ADP, про­ведённую из вер­ши­ны D, если из­вест­но, что сто­ро­на квад­ра­та равна 1.
Ре­ше­ние.

Пусть точки P и A лежат по одну сто­ро­ну от пря­мой CD (рис. 1). Тре­уголь­ник ADP — рав­но­бед­рен­ный (AD = DC = DP = 1), по­это­му

Пусть DH — вы­со­та тре­уголь­ни­ка ADP. Из пря­мо­уголь­но­го тре­уголь­ни­ка ADH на­хо­дим, что

Пусть те­перь точки P и A лежат но раз­ные сто­ро­ны от пря­мой CD (рис. 2). Тре­уголь­ник ADP — рав­но­бед­рен­ный (AD = DC = DP = 1), по­это­му

Из пря­мо­уголь­но­го тре­уголь­ни­ка ADH на­хо­дим, что

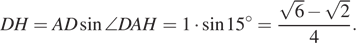
Ответ:  или .

При­ме­ча­ние.
На наш взгляд, в от­ве­те можно было оста­вить вы­ра­же­ния  и . Тем не менее, на при­ме­ре вы­чис­ле­ния зна­че­ния  ука­жем два спо­со­ба на­хож­де­ния этих ве­ли­чин:

или, ис­поль­зуя фор­му­лу по­ло­вин­но­го угла:

.

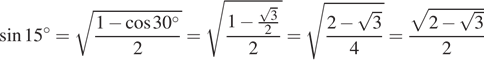За­ме­тим, кста­ти, что одно из воз­мож­ных до­ка­за­тельств ра­вен­ства по­лу­чен­ных вы­ра­же­ния сво­дит­ся к вы­де­ле­нию пол­но­го квад­ра­та из-под знака корня:

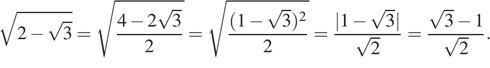
Окружности и треугольники

 В тре­уголь­ни­ке ABC, AB = 15, BC = 7, CA = 9. Точка D лежит на пря­мой BC при­чем BD : DC = 5 : 7. Окруж­но­сти, впи­сан­ные в каж­дый из тре­уголь­ни­ков ADC и ADB ка­са­ют­ся сто­ро­ны AD в точ­ках E и F. Най­ди­те длину от­рез­ка EF.
Ре­ше­ние.

Пусть AD = d, BD = x, DC = y. Ис­поль­зуя свой­ства ка­са­тель­ных, под­счи­та­ем раз­ны­ми спо­со­ба­ми пе­ри­мет­ры тре­уголь­ни­ков

От­ку­да по­лу­ча­ем:  Ана­ло­гич­но, 
Тогда 
Воз­мож­ны два слу­чая:
1. Точка D лежит на от­рез­ке BC. Тогда  зна­чит 
2. Точка D лежит вне от­рез­ка BC. Тогда  зна­чит 

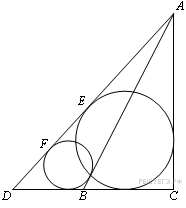
Ответ:  или 

Окружности и четырёхугольники

Че­ты­рех­уголь­ник ABCD опи­сан около окруж­но­сти и впи­сан в окруж­ность. Пря­мые AB и DC пе­ре­се­ка­ют­ся в точке M. Най­ди­те пло­щадь че­ты­рех­уголь­ни­ка, если из­вест­но, что ∠AMD = α и ра­ди­у­сы окруж­но­стей, впи­сан­ных в тре­уголь­ни­ки BCM и AMD равны со­от­вет­ствен­но r и R.
Ре­ше­ние.
Пер­вый слу­чай.
Цен­тры O1 и O окруж­но­стей, впи­сан­ных в тре­уголь­ни­ки BMC и AMD со­от­вет­ствен­но, лежат на бис­сек­три­се MO угла AMD. Окруж­ность, впи­сан­ная в че­ты­рех­уголь­ник ABCD, яв­ля­ет­ся также окруж­но­стью, впи­сан­ной в тре­уголь­ник AMD и внев­пи­сан­ной окруж­но­стью тре­уголь­ни­ка BMC. Будем ис­кать пло­щадь че­ты­рех­уголь­ни­ка ABCD, как раз­ность пло­ща­дей тре­уголь­ни­ков AMD и BMC.

Че­ты­рех­уголь­ник ABCD впи­сан в окруж­ность, сле­до­ва­тель­но, ∠BAD + ∠BCD = 180°, но ∠BCM + ∠BCD = 180°, от­ку­да ∠BCM = ∠BAD. Так как тре­уголь­ни­ки BCM и AMD имеют еще общий угол AMD, они по­доб­ны, при­чем ко­эф­фи­ци­ент по­до­бия равен от­но­ше­нию ра­ди­у­сов окруж­но­стей, впи­сан­ных в эти тре­уголь­ни­ки.
Далее имеем:
1) 
2)  где p — по­лу­пе­ри­метр тре­уголь­ни­ка BCM, рав­ный по свой­ству внев­пи­сан­ной окруж­но­сти длине от­рез­ка KM.
3) Из пря­мо­уголь­но­го тре­уголь­ни­ка OKM, на­хо­дим  от­ку­да 
Под­став­ляя най­ден­ное зна­че­ние SΔBCM в фор­му­лу SABCD, окон­ча­тель­но по­лу­ча­ем

Вто­рой слу­чай.
От­ли­ча­ет­ся от пер­во­го по­ло­же­ни­ем точки M левее точек D и A. В этом слу­чае R < r и в рас­суж­де­нии они и тре­уголь­ни­ки BCM и ADM долж­ны быть по­ме­ня­ны ме­ста­ми. Таким об­ра­зом, в этом слу­чае

 

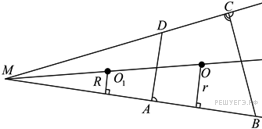
Ответ:  или 

Окружности и системы окружностей

Окруж­но­сти ра­ди­у­сов 2 и 3 с цен­тра­ми O1 и O2 со­от­вет­ствен­но ка­са­ют­ся в точке A. Пря­мая, про­хо­дя­щая через точку A, вто­рич­но пе­ре­се­ка­ет мень­шую окруж­ность в точке B, а боль­шую — в точке C. Най­ди­те пло­щадь тре­уголь­ни­ка BCO2, если ∠ABO1 = 30°.
Ре­ше­ние.

Точки O1, O2 и A лежат на одной пря­мой. По­сколь­ку тре­уголь­ни­ки BO1Aи CO2A рав­но­бед­рен­ные, ∠ABO1 = ∠BAO1 = ∠CAO2 = ∠ACО2 = 30°, от­ку­да

Воз­мож­ны два слу­чая. Пер­вый слу­чай: окруж­но­сти ка­са­ют­ся внут­рен­ним об­ра­зом (рис. 1), тогда точка B лежит между точ­ка­ми A и C, от­ку­да BC = AC − AB = 2cos30°.

Вто­рой слу­чай: окруж­но­сти ка­са­ют­ся внеш­ним об­ра­зом (рис. 2), тогда точка A лежит между точ­ка­ми B и C, от­ку­да BC = AC + AB = 10cos30°.

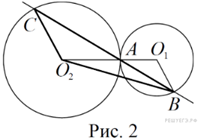
Ответ:  или .

Задача на доказательство и вычисление

Две окруж­но­сти ка­са­ют­ся внеш­ним об­ра­зом в точке K. Пря­мая AB ка­са­ет­ся пер­вой окруж­но­сти в точке A, а вто­рой — в точке B. Пря­мая BK пе­ре­се­ка­ет первую окруж­ность в точке D, пря­мая AK пе­ре­се­ка­ет вто­рую окруж­ность в точке C.
а) До­ка­жи­те, что пря­мые AD и BC па­рал­лель­ны.
б) Най­ди­те пло­щадь тре­уголь­ни­ка AKB, если из­вест­но, что ра­ди­у­сы окруж­но­стей равны 4 и 1.
Ре­ше­ние.

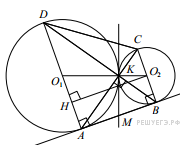
За­да­ние а). Обо­зна­чим цен­тры окруж­но­стей O1 и O2 со­от­вет­ствен­но. Пусть общая ка­са­тель­ная, про­ведённая к окруж­но­стям в точке K, пе­ре­се­ка­ет AB в точке M. По свой­ству ка­са­тель­ных, про­ведённых из одной точки, AM = KM и KM = BM. Тре­уголь­ник AKB, у ко­то­ро­го ме­ди­а­на равна по­ло­ви­не сто­ро­ны, к ко­то­рой она про­ве­де­на, — пря­мо­уголь­ный.
Впи­сан­ный угол AKD пря­мой, по­это­му он опи­ра­ет­ся на диа­метр AD. Зна­чит, AD ⊥ AB. Ана­ло­гич­но по­лу­ча­ем, что BC ⊥ AB. Сле­до­ва­тель­но, пря­мые AD и BC па­рал­лель­ны.
За­да­ние б). Пусть, для опре­де­лен­но­сти, пер­вая окруж­ность имеет ра­ди­ус 4, а ра­ди­ус вто­рой равен 1.
Тре­уголь­ни­ки BKC и AKD по­доб­ны,  Пусть , тогда 
У тре­уголь­ни­ков AKD и AKB общая вы­со­та, сле­до­ва­тель­но,  то есть SAKB = 4S. Ана­ло­гич­но, SCKD = 4S. Пло­щадь тра­пе­ции ABCD равна 25S.
Вы­чис­лим пло­щадь тра­пе­ции ABCD. Про­ведём к AD пер­пен­ди­ку­ляр O2H, рав­ный вы­со­те тра­пе­ции, и найдём его из пря­мо­уголь­но­го тре­уголь­ни­ка O2HO1:

Тогда

Сле­до­ва­тель­но, 25S = 20, от­ку­да S = 0,8 и SAKB = 4S = 3,2.

Ответ: 3,2.

Числа и их свойства

Числа и их свойства

Дано трёхзнач­ное на­ту­раль­ное число (число не может на­чи­нать­ся с нуля), не крат­ное 100.
а) Может ли част­ное этого числа и суммы его цифр быть рав­ным 90?
б) Может ли част­ное этого числа и суммы его цифр быть рав­ным 88?
в) Какое наи­боль­шее на­ту­раль­ное зна­че­ние может иметь част­ное дан­но­го числа и суммы его цифр?
Ре­ше­ние.
Пусть дан­ное число равно  где  и  — цифры сотен, де­сят­ков и еди­ниц со­от­вет­ствен­но. Если част­ное этого числа и суммы его цифр равно  то вы­пол­не­но 
а) Если част­ное равно  то   что верно, на­при­мер, при  част­ное числа  и суммы его цифр равно 
б) Если част­ное равно  то По­лу­ча­ем:  Зна­чит,  или  Но ни  ни  не де­лит­ся на  Зна­чит, част­ное трёхзнач­но­го числа и суммы его цифр не может быть рав­ным 
в) Пусть  — наи­боль­шее на­ту­раль­ное зна­че­ние част­но­го числа, не крат­но­го  и суммы его цифр. Тогда

Учи­ты­вая, что  по­лу­ча­ем:

от­ку­да 
Част­ное числа  и суммы его цифр равно  Зна­чит, наи­боль­шее на­ту­раль­ное зна­че­ние част­но­го трёхзнач­но­го числа, не крат­но­го  и суммы его цифр равно 
Ответ: а) да; б) нет; в) 91.

Числовые наборы на карточках и досках

а­ду­ма­но не­сколь­ко (не обя­за­тель­но раз­лич­ных) на­ту­раль­ных чисел. Эти числа и их все воз­мож­ные суммы (по 2, по 3 и т. д.) вы­пи­сы­ва­ют на доску в по­ряд­ке не­убы­ва­ния. Если какое-то число n, вы­пи­сан­ное на доску, по­вто­ря­ет­ся не­сколь­ко раз, то на доске остав­ля­ет­ся одно такое число n, а осталь­ные числа, рав­ные n, сти­ра­ют­ся. На­при­мер, если за­ду­ма­ны числа 1, 3, 3, 4, то на доске будет за­пи­сан набор 1, 3, 4, 5, 6, 7, 8, 10, 11.

а) При­ве­ди­те при­мер за­ду­ман­ных чисел, для ко­то­рых на доске будет за­пи­сан набор 2, 4, 6, 8, 10.
б) Су­ще­ству­ет ли при­мер таких за­ду­ман­ных чисел, для ко­то­рых на доске будет за­пи­сан набор 1, 3, 4, 5, 6, 8, 10, 11, 12, 13, 15, 17, 18, 19, 20, 22?
в) При­ве­ди­те все при­ме­ры за­ду­ман­ных чисел, для ко­то­рых на доске будет за­пи­сан набор 7, 8, 10, 15, 16, 17, 18, 23, 24, 25, 26, 31, 33, 34, 41.
Ре­ше­ние.
а) За­ду­ман­ные числа 2, 2, 2, 2, 2 дают тре­бу­е­мый набор, за­пи­сан­ный на доске.

б) По­сколь­ку за­ду­ман­ные числа на­ту­раль­ные, то наи­мень­шее число в на­бо­ре — это наи­мень­шее из за­ду­ман­ных чисел, а наи­боль­шее число в на­бо­ре — это сумма всех за­ду­ман­ных чисел. Среди чисел за­пи­сан­но­го на­бо­ра долж­на быть сумма всех чисел, кроме наи­мень­ше­го, то есть 22 − 1 = 21. Но этого числа нет в на­бо­ре, по­это­му не су­ще­ству­ет при­ме­ра таких за­ду­ман­ных чисел, для ко­то­ро­го на доске будет вы­пи­сан набор из усло­вия.

в) Число 7 — наи­мень­шее число в на­бо­ре — яв­ля­ет­ся наи­мень­шим из за­ду­ман­ных чисел, а наи­боль­шее число в на­бо­ре — это сумма всех за­ду­ман­ных чисел. По­это­му ко­ли­че­ство за­ду­ман­ных чисел не пре­вос­хо­дит целой части  , то есть 5. Кроме того, числа 8 и 10 мень­ше, чем сумма двух чисел 7, по­это­му они также яв­ля­ют­ся за­ду­ман­ны­ми. Зна­чит, сумма остав­ших­ся за­ду­ман­ных чисел равна 41 − 7 − 8 − 10 = 16. Таким об­ра­зом, так как наи­мень­шее за­ду­ман­ное число равно 7, остав­ши­е­ся за­ду­ман­ные числа — это 8 и 8 или 16. Для за­ду­ман­ных чисел 7, 8, 8, 8, 10 и 7, 8, 10, 16 на доске будет за­пи­сан набор, дан­ный в усло­вии.

Ответ: а) 2, 2, 2, 2, 2; б) нет; в) 7, 8, 8, 8, 10 или 7, 8, 10, 16.

Последовательности и прогрессии

Даны n раз­лич­ных на­ту­раль­ных чисел, со­став­ля­ю­щих ариф­ме­ти­че­скую про­грес­сию 
а) Может ли сумма всех дан­ных чисел быть рав­ной 14?
б) Ка­ко­во наи­боль­шее зна­че­ние n, если сумма всех дан­ных чисел мень­ше 900?
в) Най­ди­те все воз­мож­ные зна­че­ния n, если сумма всех дан­ных чисел равна 123.
Ре­ше­ние.
а) Да, может. Числа 2, 3, 4, 5 со­став­ля­ют ариф­ме­ти­че­скую про­грес­сию, их сумма равна 14.
б) Пусть a — пер­вый член, d — раз­ность, n — число чле­нов про­грес­сии, тогда их сумма равна  Чтобы ко­ли­че­ство чле­нов было наи­боль­шим, пер­вый член и раз­ность долж­ны быть наи­мень­ши­ми. Пусть они равны 1, тогда по усло­вию  Наи­боль­шее на­ту­раль­ное ре­ше­ние этого не­ра­вен­ства n = 41.
в) Для суммы чле­нов ариф­ме­ти­че­ской про­грес­сии имеем:

Таким об­ра­зом, число чле­нов про­грес­сии n яв­ля­ет­ся де­ли­те­лем числа 246. Если  то левая часть боль­ше 246:  сле­до­ва­тель­но,  По­сколь­ку по­лу­ча­ем, что  или  Про­грес­сии из трёх и шести чле­нов с сум­мой 123 су­ще­ству­ют: на­при­мер, 40, 41, 42 и 3, 10, 17, 24, 31, 38.

Ответ: а) да; б) 41; в) 3; 6.

 

Сюжетные задачи: кино, театр, мотки верёвки

Каж­дый из груп­пы уча­щих­ся схо­дил в кино или в театр, при этом воз­мож­но, что кто-то из них мог схо­дить и в кино, и в театр. Из­вест­но, что в те­ат­ре маль­чи­ков было не более  от об­ще­го числа уча­щих­ся груп­пы, по­се­тив­ших театр, а в кино маль­чи­ков было не более  от об­ще­го числа уча­щих­ся груп­пы, по­се­тив­ших кино.

а) Могло ли быть в груп­пе 10 маль­чи­ков, если до­пол­ни­тель­но из­вест­но, что всего в груп­пе было 20 уча­щих­ся?
б) Какое наи­боль­шее ко­ли­че­ство маль­чи­ков могло быть в груп­пе, если до­пол­ни­тель­но из­вест­но, что всего в груп­пе было 20 уча­щих­ся?
в) Какую наи­мень­шую долю могли со­став­лять де­воч­ки от об­ще­го числа уча­щих­ся в груп­пе без до­пол­ни­тель­но­го усло­вия пунк­тов а) и б)?
Ре­ше­ние.
а) Если груп­па со­сто­ит из 4 маль­чи­ков, по­се­тив­ших толь­ко театр, 6 маль­чи­ков, по­се­тив­ших толь­ко кино, и 10 де­во­чек, схо­див­ших и в театр, и в кино, то усло­вие за­да­чи вы­пол­не­но. Зна­чит, в груп­пе из 20 уча­щих­ся могло быть 10 маль­чи­ков.

б) Пред­по­ло­жим, что маль­чи­ков было 11 или боль­ше. Тогда де­во­чек было 9 или мень­ше. Театр по­се­ти­ло не более 4 маль­чи­ков, по­сколь­ку если бы их было 5 или боль­ше, то доля маль­чи­ков в те­ат­ре была бы не мень­ше , что боль­ше . Ана­ло­гич­но, кино по­се­ти­ло не более 6 маль­чи­ков, по­сколь­ку  но тогда хотя бы один маль­чик не по­се­тил ни те­ат­ра, ни кино, что про­ти­во­ре­чит усло­вию.

В преды­ду­щем пунк­те было по­ка­за­но, что в груп­пе из 20 уча­щих­ся могло быть 10 маль­чи­ков. Зна­чит, наи­боль­шее ко­ли­че­ство маль­чи­ков в груп­пе — 10.

в) Пред­по­ло­жим, что не­ко­то­рый маль­чик схо­дил и в театр, и в кино. Если бы вме­сто него в груп­пе при­сут­ство­ва­ло два маль­чи­ка, один из ко­то­рых по­се­тил толь­ко театр, а дру­гой — толь­ко кино, то доля маль­чи­ков и в те­ат­ре, и в кино оста­лась бы преж­ней, а общая доля де­во­чек стала бы мень­ше. Зна­чит, для оцен­ки наи­мень­шей доли де­во­чек в груп­пе можно счи­тать, что каж­дый маль­чик схо­дил или толь­ко в театр, или толь­ко в кино.

Пусть в груп­пе  маль­чи­ков, по­се­тив­ших театр, маль­чи­ков, по­се­тив­ших кино, и  де­во­чек. Оце­ним долю де­во­чек в этой груп­пе. Будем счи­тать, что все де­воч­ки хо­ди­ли и в театр, и в кино, по­сколь­ку их доля в груп­пе от этого не из­ме­нит­ся, а доля в те­ат­ре и в кино не умень­шит­ся.
Из усло­вия:

зна­чит,  Тогда , по­это­му доля де­во­чек в груп­пе:

Если груп­па со­сто­ит из 4 маль­чи­ков, по­се­тив­ших толь­ко театр, 6 маль­чи­ков, по­се­тив­ших толь­ко кино, и 9 де­во­чек, схо­див­ших и в театр, и в кино, то усло­вие за­да­чи вы­пол­не­но, а доля де­во­чек в груп­пе равна .

Ответ: а) да: б) 10; в) .

Примеры вариантов заданий.

Вариант 1

№	Текст задания	Вариант ответа
1.	Каж­дый день во время кон­фе­рен­ции рас­хо­ду­ет­ся 80 па­ке­ти­ков чая. Кон­фе­рен­ция длит­ся 9 дней. Чай про­да­ет­ся в пач­ках по 50 па­ке­ти­ков. Сколь­ко пачек нужно ку­пить на все дни кон­фе­рен­ции?
2.	На диа­грам­ме по­ка­за­но рас­пре­де­ле­ние вы­плав­ки меди в 10 стра­нах мира (в ты­ся­чах тонн) за 2006 год. Среди пред­став­лен­ных стран пер­вое место по вы­плав­ке меди за­ни­ма­ли США, де­ся­тое место — Ка­зах­стан. Какое место за­ни­ма­ла Ин­до­не­зия?
3.	Семья из трех че­ло­век едет из Моск­вы в Че­бок­са­ры. Можно ехать по­ез­дом, а можно — на своей ма­ши­не. Билет на поезд на од­но­го че­ло­ве­ка стоит 930 руб­лей. Ав­то­мо­биль рас­хо­ду­ет 11 лит­ров бен­зи­на на 100 ки­ло­мет­ров пути, рас­сто­я­ние по шоссе равно 700 км, а цена бен­зи­на равна 18,5 руб­лей за литр. Сколь­ко руб­лей при­дет­ся за­пла­тить за наи­бо­лее де­ше­вую по­езд­ку на троих?
4.	Диа­го­на­ли изоб­ра­жен­но­го на ри­сун­ке ромба  равны 12 и 16. Най­ди­те длину век­то­ра .
5.	В чем­пи­о­на­те мира участвуют 15 ко­манд. С по­мо­щью жре­бия их нужно раз­де­лить на пять групп по три ко­ман­ды в каж­дой. В ящике впе­ре­меш­ку лежат кар­точ­ки с но­ме­ра­ми групп:  1, 1, 1, 2, 2, 2, 3, 3, 3, 4, 4, 4, 5, 5, 5. Ка­пи­та­ны ко­манд тянут по одной кар­точ­ке. Ка­ко­ва ве­ро­ят­ность того, что ко­ман­да Рос­сии ока­жет­ся в четвёртой груп­пе?
6.	Най­ди­те ко­рень урав­не­ния: . Если урав­не­ние имеет более од­но­го корня, в от­ве­те ука­жи­те мень­ший из них.
7.	Ре­ши­те урав­не­ние . В от­ве­те на­пи­ши­те наи­мень­ший по­ло­жи­тель­ный ко­рень.
8.	В тре­уголь­ни­ке ,   — вы­со­та, . Най­ди­те .
9.	Ма­те­ри­аль­ная точка дви­жет­ся пря­мо­ли­ней­но по за­ко­ну     (где x — рас­сто­я­ние от точки от­сче­та в мет­рах, t — время в се­кун­дах, из­ме­рен­ное с на­ча­ла дви­же­ния). Най­ди­те ее ско­рость (в м/с) в мо­мент вре­ме­ни t = 3 с.
10.	Най­ди­те зна­че­ние вы­ра­же­ния .
11.	Най­ди­те зна­че­ние вы­ра­же­ния   при .
12.	Най­ди­те зна­че­ние вы­ра­же­ния .
13.	Для опре­де­ле­ния эф­фек­тив­ной тем­пе­ра­ту­ры звёзд ис­поль­зу­ют закон Сте­фа­на–Больц­ма­на, со­глас­но ко­то­ро­му мощ­ность из­лу­че­ния на­гре­то­го тела , из­ме­ря­е­мая в ват­тах, прямо про­пор­ци­о­наль­на пло­ща­ди его по­верх­но­сти и четвeртой сте­пе­ни тем­пе­ра­ту­ры: , где  – по­сто­ян­ная, пло­щадь  из­ме­ря­ет­ся в квад­рат­ных мет­рах, а тем­пе­ра­ту­ра  – в гра­ду­сах Кель­ви­на. Из­вест­но, что не­ко­то­рая звез­да имеет пло­щадь  м2, а из­лу­ча­е­мая ею мощ­ность  не менее  Вт. Опре­де­ли­те наи­мень­шую воз­мож­ную тем­пе­ра­ту­ру этой звез­ды. При­ве­ди­те ответ в гра­ду­сах Кель­ви­на.
14.	Ви­но­град со­дер­жит 90% влаги, а изюм  — 5%. Сколь­ко ки­ло­грам­мов ви­но­гра­да тре­бу­ет­ся для по­лу­че­ния 14 ки­ло­грам­мов изюма?
15.	Най­ди­те наи­мень­шее зна­че­ние функ­ции   на от­рез­ке .
16.	а) Ре­ши­те урав­не­ние б) Най­ди­те все корни этого урав­не­ния, при­над­ле­жа­щие от­рез­ку
17.	На сто­ро­не CD квад­ра­та ABCD по­стро­ен рав­но­сто­рон­ний тре­уголь­ник CPD. Най­ди­те вы­со­ту тре­уголь­ни­ка ADP, про­ведённую из вер­ши­ны D, если из­вест­но, что сто­ро­на квад­ра­та равна 1.
18.	Дано трёхзнач­ное на­ту­раль­ное число (число не может на­чи­нать­ся с нуля), не крат­ное 100. а) Может ли част­ное этого числа и суммы его цифр быть рав­ным 90? б) Может ли част­ное этого числа и суммы его цифр быть рав­ным 88? в) Какое наи­боль­шее на­ту­раль­ное зна­че­ние может иметь част­ное дан­но­го числа и суммы его цифр?

Вариант 2

№	Текст задания	Вариант ответа
1.	В доме, в ко­то­ром живет Маша, 9 эта­жей и не­сколь­ко подъ­ез­дов. На каж­дом этаже на­хо­дит­ся по 4 квар­ти­ры. Маша живет в квар­ти­ре № 130. В каком подъ­ез­де живет Маша?
2.	На диа­грам­ме по­ка­за­но ко­ли­че­ство по­се­ти­те­лей сайта РИА Но­во­сти во все дни с 10 по 29 но­яб­ря 2009 года. По го­ри­зон­та­ли ука­зы­ва­ют­ся дни ме­ся­ца, по вер­ти­ка­ли — ко­ли­че­ство по­се­ти­те­лей сайта за дан­ный день. Опре­де­ли­те по диа­грам­ме, сколь­ко раз ко­ли­че­ство по­се­ти­те­лей сайта РИА Но­во­сти при­ни­ма­ло наи­боль­шее зна­че­ние.
3.	Ке­ра­ми­че­ская плит­ка одной и той же тор­го­вой марки вы­пус­ка­ет­ся трёх раз­ных раз­ме­ров. Плит­ки упа­ко­ва­ны в пачки. Тре­бу­ет­ся ку­пить плит­ку, чтобы об­ли­це­вать пол квад­рат­ной ком­на­ты со сто­ро­ной 3 м. Раз­ме­ры плит­ки, ко­ли­че­ство пли­ток в пачке и сто­и­мость пачки при­ве­де­ны в таб­ли­це   Раз­мер плит­ки  (смсм) Ко­ли­че­ство  пли­ток в пачке Цена пачки 2020 25 604 р. 2030 16 595 р. 20 к. 3030 11 594 р.   Во сколь­ко руб­лей обойдётся наи­бо­лее дешёвый ва­ри­ант по­куп­ки?
4.	Най­ди­те цен­траль­ный угол сек­то­ра круга ра­ди­у­са   , пло­щадь ко­то­ро­го равна 1. Ответ дайте в гра­ду­сах.
5.	В слу­чай­ном экс­пе­ри­мен­те бро­са­ют три иг­раль­ные кости. Най­ди­те ве­ро­ят­ность того, что в сумме вы­па­дет 6 очков. Ре­зуль­тат округ­ли­те до сотых.
6.	Ре­ши­те урав­не­ние: .
7.	Ре­ши­те урав­не­ние .
8.	Сто­ро­на ромба равна 1, ост­рый угол равен . Най­ди­те ра­ди­ус впи­сан­ной окруж­но­сти этого ромба.
9.	На ри­сун­ке изоб­ра­жен гра­фик функ­ции , опре­де­лен­ной на ин­тер­ва­ле (−1; 13). Опре­де­ли­те ко­ли­че­ство целых точек, в ко­то­рых про­из­вод­ная функ­ции по­ло­жи­тель­на.
10.	Най­ди­те зна­че­ние вы­ра­же­ния .
11.	Най­ди­те зна­че­ние вы­ра­же­ния .
12.	Най­ди­те зна­че­ние вы­ра­же­ния .
13.	При тем­пе­ра­ту­ре   рельс имеет длину  м. При воз­рас­та­нии тем­пе­ра­ту­ры про­ис­хо­дит теп­ло­вое рас­ши­ре­ние рель­са, и его длина, вы­ра­жен­ная в мет­рах, ме­ня­ет­ся по за­ко­ну , где   — ко­эф­фи­ци­ент теп­ло­во­го рас­ши­ре­ния,   — тем­пе­ра­ту­ра (в гра­ду­сах Цель­сия). При какой тем­пе­ра­ту­ре рельс удли­нит­ся на 7,5 мм? Ответ вы­ра­зи­те в гра­ду­сах Цель­сия.
14.	Из пунк­та A в пункт B од­но­вре­мен­но вы­еха­ли два ав­то­мо­би­ля. Пер­вый про­ехал с по­сто­ян­ной ско­ро­стью весь путь. Вто­рой про­ехал первую по­ло­ви­ну пути со ско­ро­стью, мень­шей ско­ро­сти пер­во­го на 13 км/ч, а вто­рую по­ло­ви­ну пути – со ско­ро­стью 78 км/ч, в ре­зуль­та­те чего при­был в пункт В од­но­вре­мен­но с пер­вым ав­то­мо­би­лем. Най­ди­те ско­рость пер­во­го ав­то­мо­би­ля, если из­вест­но, что она боль­ше 48 км/ч. Ответ дайте в км/ч.
15.	Най­ди­те наи­мень­шее зна­че­ние функ­ции   на от­рез­ке .
16.	а) Ре­ши­те урав­не­ние:   б) Най­ди­те все корни этого урав­не­ния, при­над­ле­жа­щие про­ме­жут­ку
17.	Пря­мые, со­дер­жа­щие ка­те­ты AC и CB пря­мо­уголь­но­го тре­уголь­ни­ка АСВ, яв­ля­ют­ся об­щи­ми внут­рен­ни­ми ка­са­тель­ны­ми к окруж­но­стям ра­ди­у­сов 2 и 4. Пря­мая, со­дер­жа­щая ги­по­те­ну­зу АВ, яв­ля­ет­ся их общей внеш­ней ка­са­тель­ной. а) До­ка­жи­те, что длина от­рез­ка внут­рен­ней ка­са­тель­ной, про­ве­ден­ной из вер­ши­ны остро­го угла тре­уголь­ни­ка до одной из окруж­но­стей, равна по­ло­ви­не пе­ри­мет­ра тре­уголь­ни­ка АСВ. б) Най­ди­те пло­щадь тре­уголь­ни­ка АСВ.
18.	За­ду­ма­но не­сколь­ко (не обя­за­тель­но раз­лич­ных) на­ту­раль­ных чисел. Эти числа и их все воз­мож­ные суммы (по 2, по 3 и т. д.) вы­пи­сы­ва­ют на доску в по­ряд­ке не­убы­ва­ния. Если какое-то число n, вы­пи­сан­ное на доску, по­вто­ря­ет­ся не­сколь­ко раз, то на доске остав­ля­ет­ся одно такое число n, а осталь­ные числа, рав­ные n, сти­ра­ют­ся. На­при­мер, если за­ду­ма­ны числа 1, 3, 3, 4, то на доске будет за­пи­сан набор 1, 3, 4, 5, 6, 7, 8, 10, 11. а) При­ве­ди­те при­мер за­ду­ман­ных чисел, для ко­то­рых на доске будет за­пи­сан набор 2, 4, 6, 8, 10. б) Су­ще­ству­ет ли при­мер таких за­ду­ман­ных чисел, для ко­то­рых на доске будет за­пи­сан набор 1, 3, 4, 5, 6, 8, 10, 11, 12, 13, 15, 17, 18, 19, 20, 22? в) При­ве­ди­те все при­ме­ры за­ду­ман­ных чисел, для ко­то­рых на доске будет за­пи­сан набор 7, 8, 10, 15, 16, 17, 18, 23, 24, 25, 26, 31, 33, 34, 41.

Вариант 3

№	Текст задания	Вариант ответа
1.	Ша­ри­ко­вая ручка стоит 30 руб­лей. Какое наи­боль­шее число таких ручек можно будет ку­пить на 300 руб­лей после по­вы­ше­ния цены на 25%?
2.	В ходе хи­ми­че­ской ре­ак­ции ко­ли­че­ство ис­ход­но­го ве­ще­ства (ре­а­ген­та), ко­то­рое еще не всту­пи­ло в ре­ак­цию, со вре­ме­нем по­сте­пен­но умень­ша­ет­ся. На ри­сун­ке эта за­ви­си­мость пред­став­ле­на гра­фи­ком. На оси абс­цисс от­кла­ды­ва­ет­ся время в ми­ну­тах, про­шед­шее с мо­мен­та на­ча­ла ре­ак­ции, на оси ор­ди­нат – масса остав­ше­го­ся ре­а­ген­та, ко­то­рый еще не всту­пил в ре­ак­цию (в грам­мах). Опре­де­ли­те по гра­фи­ку, сколь­ко грам­мов ре­а­ген­та всту­пи­ло в ре­ак­цию за три ми­ну­ты?
3.	Ме­бель­ный салон за­клю­ча­ет до­го­во­ры с про­из­во­ди­те­ля­ми ме­бе­ли. В до­го­во­рах ука­зы­ва­ет­ся, какой про­цент от суммы, вы­ру­чен­ной за про­да­жу ме­бе­ли, по­сту­па­ет в доход ме­бель­но­го са­ло­на. Фирма-про­из­во­ди­тель Про­цент от вы­руч­ки, по­сту­па­ю­щий в доход са­ло­на При­ме­ча­ния «Альфа» 6,5 % Из­де­лия ценой до 20 000 руб. «Альфа» 2,5 % Из­де­лия ценой свыше 20 000 руб. «Бета» 3 % Все из­де­лия «Омик­рон» 5 % Все из­де­лия В прейс­ку­ран­те при­ве­де­ны цены на че­ты­ре крес­ла-ка­чал­ки. Опре­де­ли­те, про­да­жа ка­ко­го крес­ла-ка­чал­ки наи­бо­лее вы­год­на для са­ло­на. В ответ за­пи­ши­те, сколь­ко руб­лей по­сту­пит в доход са­ло­на от про­да­жи этого крес­ла-ка­чал­ки. Фирма-про­из­во­ди­тель Из­де­лие Цена «Альфа» Крес­ло-ка­чал­ка «Ода» 16 500 руб. «Альфа» Крес­ло-ка­чал­ка «Сага» 23 500 руб. «Бета» Крес­ло-ка­чал­ка «Поэма» 20 500 руб. «Омик­рон» Крес­ло-ка­чал­ка «Эле­гия» 18 000 руб.
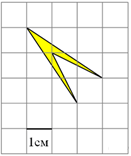
4.	Най­ди­те пло­щадь че­ты­рех­уголь­ни­ка, изоб­ра­жен­но­го на клет­ча­той бу­ма­ге с раз­ме­ром клет­ки 1 см  1 см (см. рис.). Ответ дайте в квад­рат­ных сан­ти­мет­рах.
5.	Би­ат­ло­нист 5 раз стре­ля­ет по ми­ше­ням. Ве­ро­ят­ность по­па­да­ния в ми­шень при одном вы­стре­ле равна 0,9. Най­ди­те ве­ро­ят­ность того, что би­ат­ло­нист пер­вые 4 раза попал в ми­ше­ни, а по­след­ний раз про­мах­нул­ся. Ре­зуль­тат округ­ли­те до сотых.
6.	Най­ди­те ко­рень урав­не­ния: .
7.	Най­ди­те ко­рень урав­не­ния .
8.	Ма­те­ри­аль­ная       точка       дви­жет­ся       пря­мо­ли­ней­но        по        за­ко­ну        (где  — рас­сто­я­ние от точки от­сче­та в мет­рах,  — время в се­кун­дах, из­ме­рен­ное с на­ча­ла дви­же­ния). В какой мо­мент вре­ме­ни (в се­кун­дах) ее ско­рость была равна 2 м/с?
9.	На ри­сун­ке изоб­ражён гра­фик функ­ции  — одной из пер­во­об­раз­ных не­ко­то­рой функ­ции , опре­делённой на ин­тер­ва­ле (−3;5). Поль­зу­ясь ри­сун­ком, опре­де­ли­те ко­ли­че­ство ре­ше­ний урав­не­ния  на от­рез­ке [−2;4].
10.	Най­ди­те зна­че­ние вы­ра­же­ния  .
11.	Най­ди­те зна­че­ние вы­ра­же­ния   при .
12.	Най­ди­те , если   и .
13.	Для по­лу­че­ния на экра­не уве­ли­чен­но­го изоб­ра­же­ния лам­поч­ки в ла­бо­ра­то­рии ис­поль­зу­ет­ся со­би­ра­ю­щая линза с глав­ным фо­кус­ным рас­сто­я­ни­ем  см. Рас­сто­я­ние   от линзы до лам­поч­ки может из­ме­нять­ся в пре­де­лах от 60 до 80 см, а рас­сто­я­ние  от линзы до экра­на — в пре­де­лах от 150 до 175 см. Изоб­ра­же­ние на экра­не будет чет­ким, если вы­пол­не­но со­от­но­ше­ние . Ука­жи­те, на каком наи­мень­шем рас­сто­я­нии от линзы можно по­ме­стить лам­поч­ку, чтобы еe изоб­ра­же­ние на экра­не было чeтким. Ответ вы­ра­зи­те в сан­ти­мет­рах.
14.	Из пунк­та A в пункт B од­но­вре­мен­но вы­еха­ли два ав­то­мо­би­ля. Пер­вый про­ехал с по­сто­ян­ной ско­ро­стью весь путь. Вто­рой про­ехал первую по­ло­ви­ну пути со ско­ро­стью 42 км/ч, а вто­рую по­ло­ви­ну пути — со ско­ро­стью, на 8 км/ч боль­шей ско­ро­сти пер­во­го, в ре­зуль­та­те чего при­был в В од­но­вре­мен­но с пер­вым ав­то­мо­би­лем. Най­ди­те ско­рость пер­во­го ав­то­мо­би­ля. Ответ дайте в км/ч.
15.	Най­ди­те наи­боль­шее зна­че­ние функ­ции   на от­рез­ке .
16.	а) Ре­ши­те урав­не­ние  б) Най­ди­те все корни этого урав­не­ния, при­над­ле­жа­щие от­рез­ку [−1; 2].
17.	Дан па­рал­ле­ло­грамм ABCD, AB = 3, BC = 5, ∠A = 60°. Окруж­ность с цен­тром в точке O ка­са­ет­ся бис­сек­три­сы угла D и двух сто­рон па­рал­ле­ло­грам­ма, ис­хо­дя­щих из вер­ши­ны од­но­го его остро­го угла. Най­ди­те пло­щадь четырёхуголь­ни­ка ABOD.
18.	Воз­рас­та­ю­щая ко­неч­ная ариф­ме­ти­че­ская про­грес­сия со­сто­ит из раз­лич­ных целых не­от­ри­ца­тель­ных чисел. Ма­те­ма­тик вы­чис­лил раз­ность между квад­ратом суммы всех чле­нов про­грес­сии и сум­мой их квад­ра­тов. Затем ма­те­ма­тик до­ба­вил к этой про­грес­сии сле­ду­ю­щий её член и снова вы­чис­лил такую же раз­ность. а) При­ве­ди­те при­мер такой про­грес­сии, если во вто­рой раз раз­ность ока­за­лась на 48 боль­ше, чем в пер­вый раз. б) Во вто­рой раз раз­ность ока­за­лась на 1440 боль­ше, чем в пер­вый раз. Могла ли про­грес­сия сна­ча­ла со­сто­ять из 12 чле­нов? в) Во вто­рой раз раз­ность ока­за­лась на 1440 боль­ше, чем в пер­вый раз. Какое наи­боль­шее ко­ли­че­ство чле­нов могло быть в про­грес­сии сна­ча­ла?

Вариант 4

№	Текст задания	Вариант ответа
1.	В пачке 500 ли­стов бу­ма­ги фор­ма­та А4. За не­де­лю в офисе рас­хо­ду­ет­ся 300 ли­стов. Какое наи­мень­шее ко­ли­че­ство пачек бу­ма­ги нужно ку­пить в офис на 6 не­дель?
2.	На ри­сун­ке жир­ны­ми точ­ка­ми по­ка­за­на цена пла­ти­ны, уста­нов­лен­ная Цен­тро­бан­ком РФ во все ра­бо­чие дни во все ра­бо­чие дни с 1 по 27 ок­тяб­ря 2010 года. По го­ри­зон­та­ли ука­зы­ва­ют­ся числа ме­ся­ца, по вер­ти­ка­ли — цена пла­ти­ны в руб­лях за грамм. Для на­гляд­но­сти жир­ные точки на ри­сун­ке со­еди­не­ны ли­ни­ей. Опре­де­ли­те по ри­сун­ку наи­боль­шую цену пла­ти­ны в пе­ри­од с 1 по 13 ок­тяб­ря. Ответ дайте в руб­лях за грамм.
3.	Для из­го­тов­ле­ния книж­ных полок тре­бу­ет­ся за­ка­зать 48 оди­на­ко­вых сте­кол в одной из трех фирм. Пло­щадь каж­до­го стек­ла 0,25 м2. В таб­ли­це при­ве­де­ны цены на стек­ло, а также на резку сте­кол и шли­фов­ку края. Сколь­ко руб­лей будет сто­ить самый де­ше­вый заказ?  Фирма Цена стек­ла (руб. за 1 м2) Резка и шли­фов­ка (руб. за одно стек­ло) A 420 75 Б 440 65 В 470 55
4.	Най­ди­те пло­щадь сек­то­ра круга ра­ди­у­са 1, длина дуги ко­то­ро­го равна 2.
5.	Перед на­ча­лом пер­во­го тура чем­пи­о­на­та по бад­мин­то­ну участ­ни­ков раз­би­ва­ют на иг­ро­вые пары слу­чай­ным об­ра­зом с по­мо­щью жре­бия. Всего в чем­пи­о­на­те участ­ву­ет 26 бад­мин­то­ни­стов, среди ко­то­рых 10 участ­ни­ков из Рос­сии, в том числе Рус­лан Орлов. Най­ди­те ве­ро­ят­ность того, что в пер­вом туре Рус­лан Орлов будет иг­рать с каким-либо бад­мин­то­ни­стом из Рос­сии?
6.	Ре­ши­те урав­не­ние . Если урав­не­ние имеет более од­но­го корня, в от­ве­те за­пи­ши­те боль­ший из кор­ней.
7.	Най­ди­те корни урав­не­ния: . В ответ за­пи­ши­те наи­боль­ший от­ри­ца­тель­ный ко­рень.
8.	В тре­уголь­ни­ке   угол   равен 90°,  – вы­со­та, , . Най­ди­те .
9.	Ма­те­ри­аль­ная точка дви­жет­ся пря­мо­ли­ней­но по за­ко­ну   (где  — рас­сто­я­ние от точки от­сче­та в мет­рах,  — время в се­кун­дах, из­ме­рен­ное с на­ча­ла дви­же­ния). Най­ди­те ее ско­рость в (м/с) в мо­мент вре­ме­ни  с.
10.	Най­ди­те зна­че­ние вы­ра­же­ния .
11.	Най­ди­те зна­че­ние вы­ра­же­ния   при .
12.	Най­ди­те зна­че­ние вы­ра­же­ния  .
13.	Для под­дер­жа­ния на­ве­са пла­ни­ру­ет­ся ис­поль­зо­вать ци­лин­дри­че­скую ко­лон­ну. Дав­ле­ние  (в пас­ка­лях), ока­зы­ва­е­мое на­ве­сом и ко­лон­ной на опору, опре­де­ля­ет­ся по фор­му­ле , где   кг — общая масса на­ве­са и ко­лон­ны,  — диа­метр ко­лон­ны (в мет­рах). Счи­тая уско­ре­ние сво­бод­но­го па­де­ния   м/с2, а , опре­де­ли­те наи­мень­ший воз­мож­ный диа­метр ко­лон­ны, если дав­ле­ние, ока­зы­ва­е­мое на опору, не долж­но быть боль­ше 800 000 Па. Ответ вы­ра­зи­те в мет­рах.
14.	Сме­шав 30-про­цент­ный и 60-про­цент­ный рас­тво­ры кис­ло­ты и до­ба­вив 10 кг чи­стой воды, по­лу­чи­ли 36-про­цент­ный рас­твор кис­ло­ты. Если бы вме­сто 10 кг воды до­ба­ви­ли 10 кг 50-про­цент­но­го рас­тво­ра той же кис­ло­ты, то по­лу­чи­ли бы 41-про­цент­ный рас­твор кис­ло­ты. Сколь­ко ки­ло­грам­мов 30-про­цент­но­го рас­тво­ра ис­поль­зо­ва­ли для по­лу­че­ния смеси?
15.	Най­ди­те наи­мень­шее зна­че­ние функ­ции   на от­рез­ке .
16.	Ре­ши­те урав­не­ние:
17.	Центр O окруж­но­сти ра­ди­у­са 4 при­над­ле­жит бис­сек­три­се угла ве­ли­чи­ной 60°. Най­ди­те ра­ди­ус окруж­но­сти, впи­сан­ной в дан­ный угол и ка­са­ю­щей­ся дан­ной окруж­но­сти, если из­вест­но, что рас­сто­я­ние от точки O до вер­ши­ны угла равно 10.
18.	В игре «Дро­ти­ки» есть 20 на­руж­ных сек­то­ров, про­ну­ме­ро­ван­ных от 1 до 20 и два цен­траль­ных сек­то­ра. При по­па­да­нии в на­руж­ный сек­тор игрок по­лу­ча­ет ко­ли­че­ство очков, сов­па­да­ю­щее с но­ме­ром сек­то­ра, а за по­па­да­ние в цен­траль­ные сек­то­ра он по­лу­ча­ет 25 или 50 очков со­от­вет­ствен­но. В каж­дом из на­руж­ных сек­то­ров есть об­ла­сти удво­е­ния и утро­е­ния, ко­то­рые, со­от­вет­ствен­но, удва­и­ва­ют или утра­и­ва­ют но­ми­нал сек­то­ра. Так, на­при­мер, по­па­да­ние в сек­тор 10 (не в зоны удво­е­ния и утро­е­ния) дает 10 очков, в зону удво­е­ния сек­то­ра ― 20 очков, в зону утро­е­ния ― 30 очков. а) Может ли игрок тремя брос­ка­ми на­брать ровно 167 очков? б) Может ли игрок ше­стью брос­ка­ми на­брать ровно 356 очков? в) С по­мо­щью ка­ко­го наи­мень­ше­го ко­ли­че­ства брос­ков, игрок может на­брать ровно 1001 очко?

Вариант 5

№	Текст задания	Вариант ответа
1.	Фут­бол­ка сто­и­ла 800 руб­лей. После сни­же­ния цены она стала сто­ить 680 руб­лей. На сколь­ко про­цен­тов была сни­же­на цена на фут­бол­ку?
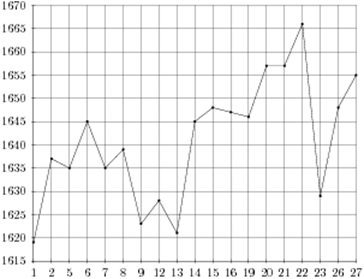
2.	На ри­сун­ке по­ка­за­но из­ме­не­ние тем­пе­ра­ту­ры воз­ду­ха на про­тя­же­нии трех суток. По го­ри­зон­та­ли ука­зы­ва­ет­ся дата и время суток, по вер­ти­ка­ли — зна­че­ние тем­пе­ра­ту­ры в гра­ду­сах Цель­сия. Опре­де­ли­те по ри­сун­ку наи­боль­шую тем­пе­ра­ту­ру воз­ду­ха 19 фев­ра­ля. Ответ дайте в гра­ду­сах Цель­сия.
3.	Для груп­пы ино­стран­ных го­стей тре­бу­ет­ся ку­пить 10 пу­те­во­ди­те­лей. Нуж­ные пу­те­во­ди­те­ли на­шлись в трёх ин­тер­нет-ма­га­зи­нах. Усло­вия по­куп­ки и до­став­ки даны в таб­ли­це. Ин­тер­нет-  ма­га­зин Цена од­но­го  пу­те­во­ди­те­ля (руб.) Сто­и­мость  до­став­ки (руб.) До­пол­ни­тель­ные усло­вия А 283 200 Нет Б 271 300 До­став­ка бес­плат­но, если  сумма за­ка­за пре­вы­ша­ет 3000 руб. В 302 250 До­став­ка бес­плат­но, если  сумма за­ка­за пре­вы­ша­ет 2500 руб. Опре­де­ли­те, в каком из ма­га­зи­нов общая сумма по­куп­ки с учётом до­став­ки будет наи­мень­шей. В ответ за­пи­ши­те наи­мень­шую сумму в руб­лях.
4.	Най­ди­те пло­щадь че­ты­рех­уголь­ни­ка, изоб­ра­жен­но­го на клет­ча­той бу­ма­ге с раз­ме­ром клет­ки 1 см  1 см (см. рис.). Ответ дайте в квад­рат­ных сан­ти­мет­рах.
5.	В фирме такси в на­ли­чии 50 лег­ко­вых ав­то­мо­би­лей; 27 из них чёрные с жёлтыми над­пи­ся­ми на бор­тах, осталь­ные — жёлтые с чёрными над­пи­ся­ми. Най­ди­те ве­ро­ят­ность того, что на слу­чай­ный вызов при­е­дет ма­ши­на жёлтого цвета с чёрными над­пи­ся­ми.
6.	Най­ди­те ко­рень урав­не­ния:  . Если урав­не­ние имеет более од­но­го корня, в от­ве­те ука­жи­те боль­ший из них.
7.	Ре­ши­те урав­не­ние . В от­ве­те на­пи­ши­те наи­боль­ший от­ри­ца­тель­ный ко­рень.
8.	В тре­уголь­ни­ке  угол   равен ,   – вы­со­та,, . Най­ди­те .
9.	На ри­сун­ке  изоб­ра­жен  гра­фик  про­из­вод­ной  функ­ции .  Най­ди­те  абс­цис­су точки,  в  ко­то­рой  ка­са­тель­ная   к гра­фи­ку    па­рал­лель­на пря­мой   или сов­па­да­ет с ней.
10.	Най­ди­те зна­че­ние вы­ра­же­ния  .
11.	Най­ди­те зна­че­ние вы­ра­же­ния   при .
12.	Най­ди­те зна­че­ние вы­ра­же­ния .
13.	В ро­зет­ку элек­тро­се­ти под­клю­че­ны при­бо­ры, общее со­про­тив­ле­ние ко­то­рых со­став­ля­ет   Ом. Па­рал­лель­но с ними в ро­зет­ку пред­по­ла­га­ет­ся под­клю­чить элек­тро­обо­гре­ва­тель. Опре­де­ли­те наи­мень­шее воз­мож­ное со­про­тив­ле­ние   этого элек­тро­обо­гре­ва­те­ля, если из­вест­но, что при па­рал­лель­ном со­еди­не­нии двух про­вод­ни­ков с со­про­тив­ле­ни­я­ми   Ом и  Ом их общее со­про­тив­ле­ние даётся фор­му­лой  (Ом), а для нор­маль­но­го функ­ци­о­ни­ро­ва­ния элек­тро­се­ти общее со­про­тив­ле­ние в ней долж­но быть не мень­ше 9 Ом. Ответ вы­ра­зи­те в омах.
14.	По­ло­ви­ну вре­ме­ни, за­тра­чен­но­го на до­ро­гу, ав­то­мо­биль ехал со ско­ро­стью 67 км/ч, а вто­рую по­ло­ви­ну вре­ме­ни — со ско­ро­стью 79 км/ч. Най­ди­те сред­нюю ско­рость ав­то­мо­би­ля на про­тя­же­нии всего пути. Ответ дайте в км/ч.
15.	Най­ди­те наи­боль­шее зна­че­ние функ­ции   на от­рез­ке .
16.	а) Ре­ши­те урав­не­ние   б) Най­ди­те все корни этого урав­не­ния, при­над­ле­жа­щие от­рез­ку
17.	Ме­ди­а­ны AA1, BB1 и CC1 тре­уголь­ни­ка ABC пе­ре­се­ка­ют­ся в точке M. Точки A2, B2 и C2 — се­ре­ди­ны от­рез­ков MA, MB и MC со­от­вет­ствен­но. а) До­ка­жи­те, что пло­щадь ше­сти­уголь­ни­ка A1B2C1A2B1C2 вдвое мень­ше пло­ща­ди тре­уголь­ни­ка ABC. б) Най­ди­те сумму квад­ра­тов всех сто­рон этого ше­сти­уголь­ни­ка, если из­вест­но, что AB = 5, BC = 8 и AC = 10.
18.	Най­ди­те все трой­ки на­ту­раль­ных чисел k, m и n, удо­вле­тво­ря­ю­щие урав­не­нию

Ответы на задания примеров вариантов.

Ответы на задания 1-15

	1	2	3	4	5
1	15	4	8	4	15
2	5	3	12	1645	-2
3	1424,5	5436	1072,5	8280	3010
4	16	22,5	1	1	3
5	0,2	0,05	0,07	0,36	0,46
6	-3	-7	1	5	5
7	0,5	-2	-5	-4	-1
8	24	0,25	7	27	12,5
9	8	3	10	59	5
10	7	-12	24	0,75	2
11	0,8	2	343	2,5	12
12	-1,25	0,1	-0,75	2	-1
13	4000	62,5	70	0,2	10
14	133	52	48	60	73
15	-54	15	900	0	11
	1	2	3	4	5

Ответы на задание 16.

а) Ре­ши­те урав­не­ние

б) Най­ди­те все корни этого урав­не­ния, при­над­ле­жа­щие от­рез­ку 
Ре­ше­ние.
Сде­ла­ем за­ме­ну 

 Тогда, 

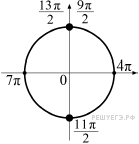б) При по­мо­щи три­го­но­мет­ри­че­ской окруж­но­сти отберём корни, ле­жа­щие на от­рез­ке 

Ответ: а)  б) 

а) Ре­ши­те урав­не­ние:

б) Най­ди­те все корни этого урав­не­ния, при­над­ле­жа­щие про­ме­жут­ку 
Ре­ше­ние.
Ис­поль­зуя фор­му­лу при­ве­де­ния  и фор­му­лу си­ну­са двой­но­го угла , по­лу­ча­ем:

За­дан­ный про­ме­жу­ток имеет длину π, по­это­му ему при­над­ле­жит не боль­ше двух кор­ней из пер­вой серии, не боль­ше од­но­го корня из вто­рой серии и не боль­ше од­но­го корня из тре­тьей серии. Во вто­рой серии ре­ше­ний из от­рез­ка нет, из пер­вой и тре­тьей серии это числа 
Ответ: а)  б) 

а) Ре­ши­те урав­не­ние 

б) Най­ди­те все корни этого урав­не­ния, при­над­ле­жа­щие от­рез­ку [−1; 2].
Ре­ше­ние.
а) Пре­об­ра­зу­ем урав­не­ние:


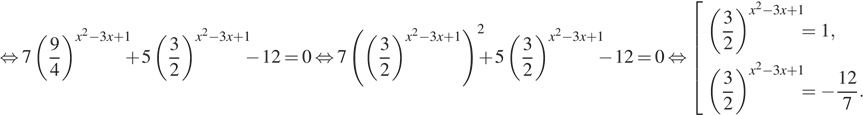
У вто­ро­го урав­не­ния ре­ше­ний нет.
Пре­об­ра­зу­ем пер­вое урав­не­ние:  от­ку­да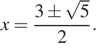 
б) Оце­ним  це­лы­ми чис­ла­ми:  Тогда

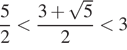 и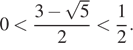 

Зна­чит, от­рез­ку  при­над­ле­жит толь­ко 

Ответ: а) 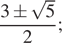 б) 

 

Ре­ши­те урав­не­ние: 

Ре­ше­ние.
Урав­не­ние рав­но­силь­но си­сте­ме:

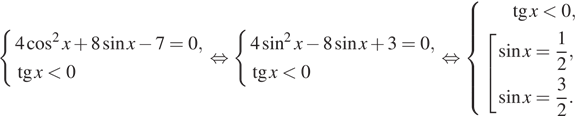
Урав­не­ние  ре­ше­ний не имеет. Учи­ты­вая, что  по­лу­ча­ем: 

Ответ: 

а) Ре­ши­те урав­не­ние 

 

б) Най­ди­те все корни этого урав­не­ния, при­над­ле­жа­щие от­рез­ку 
Ре­ше­ние.
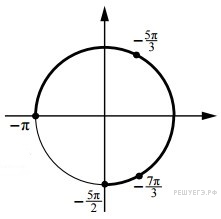а) По­сле­до­ва­тель­но по­лу­ча­ем:

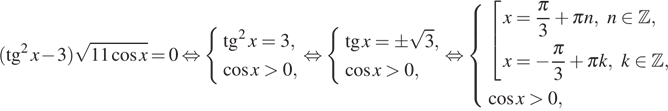
от­ку­да  или 

б) Корни, при­над­ле­жа­щие от­рез­ку  отберём с по­мо­щью еди­нич­ной окруж­но­сти.
По­лу­ча­ем  и 

Ответ: а)  б) 

Ответы на задание 17.

На сто­ро­не CD квад­ра­та ABCD по­стро­ен рав­но­сто­рон­ний тре­уголь­ник CPD. Най­ди­те вы­со­ту тре­уголь­ни­ка ADP, про­ведённую из вер­ши­ны D, если из­вест­но, что сто­ро­на квад­ра­та равна 1.

Ре­ше­ние.

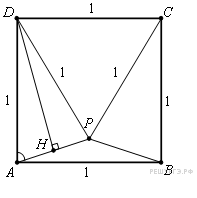
Пусть точки P и A лежат по одну сто­ро­ну от пря­мой CD (рис. 1). Тре­уголь­ник ADP — рав­но­бед­рен­ный (AD = DC = DP = 1), по­это­му

Пусть DH — вы­со­та тре­уголь­ни­ка ADP. Из пря­мо­уголь­но­го тре­уголь­ни­ка ADH на­хо­дим, что

Пусть те­перь точки P и A лежат но раз­ные сто­ро­ны от пря­мой CD (рис. 2). Тре­уголь­ник ADP — рав­но­бед­рен­ный (AD = DC = DP = 1), по­это­му

Из пря­мо­уголь­но­го тре­уголь­ни­ка ADH на­хо­дим, что

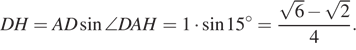
Ответ:  или .

Пря­мые, со­дер­жа­щие ка­те­ты AC и CB пря­мо­уголь­но­го тре­уголь­ни­ка АСВ, яв­ля­ют­ся об­щи­ми внут­рен­ни­ми ка­са­тель­ны­ми к окруж­но­стям ра­ди­у­сов 2 и 4. Пря­мая, со­дер­жа­щая ги­по­те­ну­зу АВ, яв­ля­ет­ся их общей внеш­ней ка­са­тель­ной.

а) До­ка­жи­те, что длина от­рез­ка внут­рен­ней ка­са­тель­ной, про­ве­ден­ной из вер­ши­ны остро­го угла тре­уголь­ни­ка до одной из окруж­но­стей, равна по­ло­ви­не пе­ри­мет­ра тре­уголь­ни­ка АСВ.
б) Най­ди­те пло­щадь тре­уголь­ни­ка АСВ.
Ре­ше­ние.
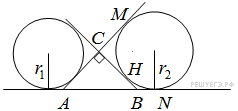а) Введём обо­зна­че­ния, как по­ка­за­но на ри­сун­ке, пусть M, H, N — точки ка­са­ния. Ка­са­тель­ные, про­ведённые к окруж­но­сти из одной точки равны: AM = AN, CM = CH, HB = BN. По­это­му:

от­ку­да p = AM.
б) Для опре­де­ле­ния пло­ща­ди тре­уголь­ни­ка ис­поль­зу­ем фор­му­лу, свя­зы­ва­ю­щую её с по­лу­пе­ри­мет­ром, сто­ро­ной и ра­ди­у­сом внев­пи­сан­ной окруж­но­сти, ка­са­ю­щей­ся этой сто­ро­ны и про­дол­же­ний двух дру­гих сто­рон тре­уголь­ни­ка:

 

Дан па­рал­ле­ло­грамм ABCD, AB = 3, BC = 5, ∠A = 60°. Окруж­ность с цен­тром в точке O ка­са­ет­ся бис­сек­три­сы угла D и двух сто­рон па­рал­ле­ло­грам­ма, ис­хо­дя­щих из вер­ши­ны од­но­го его остро­го угла. Най­ди­те пло­щадь четырёхуголь­ни­ка ABOD.

Ре­ше­ние.

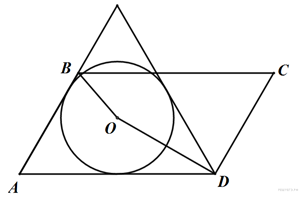
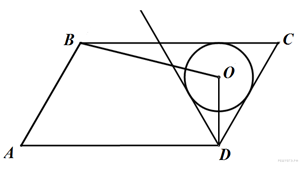
Окруж­но­стей две: каж­дая из них впи­сан­ная в пра­виль­ный тре­уголь­ник. Эти тре­уголь­ни­ки имеют сто­ро­ны рав­ные 5 и 3 — со­от­вет­ствен­но. По­это­му ра­ди­у­сы окруж­но­стей равны тре­тьей части вы­со­ты пра­виль­но­го тре­уголь­ни­ка.
Для тре­уголь­ни­ка со сто­ро­ной 5 ра­ди­ус равен 
Най­дем пло­щадь не­вы­пук­ло­го че­ты­рех­уголь­ни­ка как сумму пло­ща­дей тре­уголь­ни­ков AOB и AOD:

Для тре­уголь­ни­ка со сто­ро­ной 3 ра­ди­ус равен 
Чтобы найти пло­щадь че­ты­рех­уголь­ни­ка ABOD, вы­чтем из пло­ща­ди па­рал­ле­ло­грам­ма пло­ща­ди тре­уголь­ни­ков BOC и DOC:

 

Ответ:  или 

Центр O окруж­но­сти ра­ди­у­са 4 при­над­ле­жит бис­сек­три­се угла ве­ли­чи­ной 60°. Най­ди­те ра­ди­ус окруж­но­сти, впи­сан­ной в дан­ный угол и ка­са­ю­щей­ся дан­ной окруж­но­сти, если из­вест­но, что рас­сто­я­ние от точки O до вер­ши­ны угла равно 10.

Ре­ше­ние.
Пусть Q — центр ис­ко­мой окруж­но­сти ра­ди­у­са x, B — точка ка­са­ния одной из сто­рон дан­но­го угла с вер­ши­ной A. Центр окруж­но­сти, впи­сан­ной в угол, лежит на бис­сек­три­се угла, по­это­му ∠BAQ = 30°. Из пря­мо­уголь­но­го тре­уголь­ни­ка BAQ на­хо­дим, что AQ = 2QB = 2x. Рас­смот­рим слу­чай внеш­не­го ка­са­ния окруж­но­стей. Если точка Q лежит между A и O (см. рис.), то AO = AQ + QO, или 10 = 2x + (x + 4), от­ку­да на­хо­дим, что x = 2.

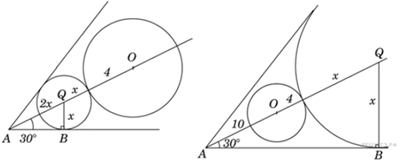
Если точка O лежит между A и Q (см. рис.), то AQ = AO + OQ, или 2x = 10 + (4 − x), от­ку­да x = 14.
Рас­смот­рим слу­чай внут­рен­не­го ка­са­ния окруж­но­стей. Если точка Q лежит между A и O (см. рис.), то AO = AQ + QO, или 10 = 2x + (x − 4), от­ку­да на­хо­дим, что 

Если точка O лежит между A и Q (см. рис.), то AQ = AO + OQ, или 2x = 10 + (x  4), от­ку­да x = 6.

Ответ: 2; 14;  6.

Ме­ди­а­ны AA1, BB1 и CC1 тре­уголь­ни­ка ABC пе­ре­се­ка­ют­ся в точке M. Точки A2, B2 и C2 — се­ре­ди­ны от­рез­ков MA, MB и MC со­от­вет­ствен­но.

а) До­ка­жи­те, что пло­щадь ше­сти­уголь­ни­ка A1B2C1A2B1C2 вдвое мень­ше пло­ща­ди тре­уголь­ни­ка ABC.
б) Най­ди­те сумму квад­ра­тов всех сто­рон этого ше­сти­уголь­ни­ка, если из­вест­но, что AB = 5, BC = 8 и AC = 10.
Ре­ше­ние.
а) Пло­щадь тре­уголь­ни­ка A1MB2 в два раза мень­ше пло­ща­ди тре­уголь­ни­ка A1MB, по­сколь­ку MB = 2MB2, а вы­со­та, про­ведённая из вер­ши­ны A1, у этих тре­уголь­ни­ков общая:

Ана­ло­гич­но по­лу­ча­ем ещё 5 ра­венств:

 и 

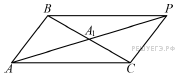Скла­ды­вая эти ра­вен­ства почлен­но, по­лу­ча­ем

б) Обо­зна­чим длины сто­рон BC, AC, AB тре­уголь­ни­ка ABC через a, b, c.
До­ка­жем, что квад­рат ме­ди­а­ны AA1 равен  Для до­ка­за­тель­ства на про­дол­же­нии от­рез­ка AA1 за точку A1 от­ло­жим от­ре­зок A1P = AA1. По­лу­чим па­рал­ле­ло­грамм ACPB со сто­ро­на­ми AC = PB = b и AB = CP = c и диа­го­на­ля­ми BC = a и AP = 2AA1. Сумма квад­ра­тов диа­го­на­лей па­рал­ле­ло­грам­ма равна сумме квад­ра­тов его сто­рон:  от­ку­да  Ана­ло­гич­но до­ка­зы­ва­ет­ся, что  а 
От­ре­зок C1A2 — сред­няя линия тре­уголь­ни­ка ABM, зна­чит,

Рас­суж­дая ана­ло­гич­но, мы по­лу­чим, что сто­ро­ны ше­сти­уголь­ни­ка втрое мень­ше ме­ди­ан тре­уголь­ни­ка

Сле­до­ва­тель­но, сумма квад­ра­тов сто­рон ше­сти­уголь­ни­ка равна

Под­став­ляя в эту фор­му­лу длины сто­рон тре­уголь­ни­ка ABC, по­лу­ча­ем 

Ответ: 

Ответы на задание 18.

Дано трёхзнач­ное на­ту­раль­ное число (число не может на­чи­нать­ся с нуля), не крат­ное 100.

а) Может ли част­ное этого числа и суммы его цифр быть рав­ным 90?
б) Может ли част­ное этого числа и суммы его цифр быть рав­ным 88?
в) Какое наи­боль­шее на­ту­раль­ное зна­че­ние может иметь част­ное дан­но­го числа и суммы его цифр?
Ре­ше­ние.
Пусть дан­ное число равно  где  и  — цифры сотен, де­сят­ков и еди­ниц со­от­вет­ствен­но. Если част­ное этого числа и суммы его цифр равно  то вы­пол­не­но 
а) Если част­ное равно  то   что верно, на­при­мер, при  част­ное числа  и суммы его цифр равно 
б) Если част­ное равно  то По­лу­ча­ем:  Зна­чит,  или  Но ни  ни  не де­лит­ся на  Зна­чит, част­ное трёхзнач­но­го числа и суммы его цифр не может быть рав­ным 
в) Пусть  — наи­боль­шее на­ту­раль­ное зна­че­ние част­но­го числа, не крат­но­го  и суммы его цифр. Тогда

Учи­ты­вая, что  по­лу­ча­ем:

от­ку­да 
Част­ное числа  и суммы его цифр равно  Зна­чит, наи­боль­шее на­ту­раль­ное зна­че­ние част­но­го трёхзнач­но­го числа, не крат­но­го  и суммы его цифр равно 
Ответ: а) да; б) нет; в) 91.

За­ду­ма­но не­сколь­ко (не обя­за­тель­но раз­лич­ных) на­ту­раль­ных чисел. Эти числа и их все воз­мож­ные суммы (по 2, по 3 и т. д.) вы­пи­сы­ва­ют на доску в по­ряд­ке не­убы­ва­ния. Если какое-то число n, вы­пи­сан­ное на доску, по­вто­ря­ет­ся не­сколь­ко раз, то на доске остав­ля­ет­ся одно такое число n, а осталь­ные числа, рав­ные n, сти­ра­ют­ся. На­при­мер, если за­ду­ма­ны числа 1, 3, 3, 4, то на доске будет за­пи­сан набор 1, 3, 4, 5, 6, 7, 8, 10, 11.

 

а) При­ве­ди­те при­мер за­ду­ман­ных чисел, для ко­то­рых на доске будет за­пи­сан набор 2, 4, 6, 8, 10.
б) Су­ще­ству­ет ли при­мер таких за­ду­ман­ных чисел, для ко­то­рых на доске будет за­пи­сан набор 1, 3, 4, 5, 6, 8, 10, 11, 12, 13, 15, 17, 18, 19, 20, 22?
в) При­ве­ди­те все при­ме­ры за­ду­ман­ных чисел, для ко­то­рых на доске будет за­пи­сан набор 7, 8, 10, 15, 16, 17, 18, 23, 24, 25, 26, 31, 33, 34, 41.
Ре­ше­ние.
а) За­ду­ман­ные числа 2, 2, 2, 2, 2 дают тре­бу­е­мый набор, за­пи­сан­ный на доске.

б) По­сколь­ку за­ду­ман­ные числа на­ту­раль­ные, то наи­мень­шее число в на­бо­ре — это наи­мень­шее из за­ду­ман­ных чисел, а наи­боль­шее число в на­бо­ре — это сумма всех за­ду­ман­ных чисел. Среди чисел за­пи­сан­но­го на­бо­ра долж­на быть сумма всех чисел, кроме наи­мень­ше­го, то есть 22 − 1 = 21. Но этого числа нет в на­бо­ре, по­это­му не су­ще­ству­ет при­ме­ра таких за­ду­ман­ных чисел, для ко­то­ро­го на доске будет вы­пи­сан набор из усло­вия.

в) Число 7 — наи­мень­шее число в на­бо­ре — яв­ля­ет­ся наи­мень­шим из за­ду­ман­ных чисел, а наи­боль­шее число в на­бо­ре — это сумма всех за­ду­ман­ных чисел. По­это­му ко­ли­че­ство за­ду­ман­ных чисел не пре­вос­хо­дит целой части  , то есть 5. Кроме того, числа 8 и 10 мень­ше, чем сумма двух чисел 7, по­это­му они также яв­ля­ют­ся за­ду­ман­ны­ми. Зна­чит, сумма остав­ших­ся за­ду­ман­ных чисел равна 41 − 7 − 8 − 10 = 16. Таким об­ра­зом, так как наи­мень­шее за­ду­ман­ное число равно 7, остав­ши­е­ся за­ду­ман­ные числа — это 8 и 8 или 16. Для за­ду­ман­ных чисел 7, 8, 8, 8, 10 и 7, 8, 10, 16 на доске будет за­пи­сан набор, дан­ный в усло­вии.

Ответ: а) 2, 2, 2, 2, 2; б) нет; в) 7, 8, 8, 8, 10 или 7, 8, 10, 16.

Воз­рас­та­ю­щая ко­неч­ная ариф­ме­ти­че­ская про­грес­сия со­сто­ит из раз­лич­ных целых не­от­ри­ца­тель­ных чисел. Ма­те­ма­тик вы­чис­лил раз­ность между квад­ратом суммы всех чле­нов про­грес­сии и сум­мой их квад­ра­тов. Затем ма­те­ма­тик до­ба­вил к этой про­грес­сии сле­ду­ю­щий её член и снова вы­чис­лил такую же раз­ность.

а) При­ве­ди­те при­мер такой про­грес­сии, если во вто­рой раз раз­ность ока­за­лась на 48 боль­ше, чем в пер­вый раз.
б) Во вто­рой раз раз­ность ока­за­лась на 1440 боль­ше, чем в пер­вый раз. Могла ли про­грес­сия сна­ча­ла со­сто­ять из 12 чле­нов?
в) Во вто­рой раз раз­ность ока­за­лась на 1440 боль­ше, чем в пер­вый раз. Какое наи­боль­шее ко­ли­че­ство чле­нов могло быть в про­грес­сии сна­ча­ла?
Ре­ше­ние.
а) При­мер: 1, 2, 3. Раз­ность квад­ра­та суммы и суммы квад­ра­тов равна 36 − 14 = 22. Если до­ба­вить число 4, то раз­ность будет равна 100 − 30 = 70, что ровно на 48 боль­ше, чем было.
б) Обо­зна­чим члены про­грес­сии a1, a2,...,an. Тогда раз­ность, вы­чи­лен­ная ма­те­ма­ти­ком в пер­вый раз, равна

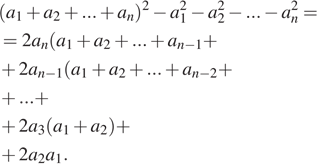
Когда к про­грес­сии до­ба­ви­ли член an+1, то вы­чис­лен­ная во вто­рой раз раз­ность от­ли­ча­ет­ся от пер­вой до­пол­ни­тель­ным сла­га­е­мым

где d — раз­ность про­грес­сии.
Из усло­вия сле­ду­ет, что  и  по­это­му

По­лу­ча­ем не­ра­вен­ство

от­ку­да  Зна­чит, 12 чле­нов в на­чаль­ной про­грес­сии быть не может.
в) Из ра­вен­ства  сле­ду­ет, что n яв­ля­ет­ся де­ли­те­лем числа 1440. Зна­чит, 
Если n = 10, по­лу­ча­ем

Если  то левая часть не мень­ше чем 
Сле­до­ва­тель­но, d = 1. По­лу­ча­ем урав­не­ние

ко­то­рое не имеет целых ре­ше­ний.
Если n = 9, по­лу­ча­ем

Если  то левая часть не мень­ше чем 
Сле­до­ва­тель­но, d = 1. По­лу­ча­ем урав­не­ние

ко­то­рое не имеет целых ре­ше­ний.
Если n = 8, по­лу­ча­ем:

Если  то левая часть не мень­ше чем 
Сле­до­ва­тель­но, d = 1. По­лу­ча­ем урав­не­ние

ко­то­рое имеет един­ствен­ный на­ту­раль­ный ко­рень 4.
Зна­чит, про­грес­сия из вось­ми чисел 4, 5, 6, ..., 11 удо­вле­тво­ря­ют усло­вию за­да­чи.

Ответ: а) 1, 2, 3; б) нет; в) 8.

В игре «Дро­ти­ки» есть 20 на­руж­ных сек­то­ров, про­ну­ме­ро­ван­ных от 1 до 20 и два цен­траль­ных сек­то­ра. При по­па­да­нии в на­руж­ный сек­тор игрок по­лу­ча­ет ко­ли­че­ство очков, сов­па­да­ю­щее с но­ме­ром сек­то­ра, а за по­па­да­ние в цен­траль­ные сек­то­ра он по­лу­ча­ет 25 или 50 очков со­от­вет­ствен­но. В каж­дом из на­руж­ных сек­то­ров есть об­ла­сти удво­е­ния и утро­е­ния, ко­то­рые, со­от­вет­ствен­но, удва­и­ва­ют или утра­и­ва­ют но­ми­нал сек­то­ра. Так, на­при­мер, по­па­да­ние в сек­тор 10 (не в зоны удво­е­ния и утро­е­ния) дает 10 очков, в зону удво­е­ния сек­то­ра ― 20 очков, в зону утро­е­ния ― 30 очков.

а) Может ли игрок тремя брос­ка­ми на­брать ровно 167 очков?
б) Может ли игрок ше­стью брос­ка­ми на­брать ровно 356 очков?
в) С по­мо­щью ка­ко­го наи­мень­ше­го ко­ли­че­ства брос­ков, игрок может на­брать ровно 1001 очко?
Ре­ше­ние.
а) Да, на­при­мер, при по­па­да­нии в утро­е­ние сек­то­ра 20, утро­е­ние сек­то­ра 19 и цен­траль­ный сек­тор 50 по­лу­ча­ем: 60 + 57 + 50 = 167.
б) Наи­боль­шее ко­ли­че­ство очков, ко­то­рое может на­брать игрок одним брос­ком ― 60 (утро­е­ние 20), далее идут: 57 очков (утро­е­ние 19) и 54 очка (утро­е­ние 18). По­па­да­ние во все осталь­ные сек­то­ра и зоны дает мень­ше 54 очков. Если все шесть брос­ков были по 60 очков, то игрок на­брал 360 очков, что боль­ше 356. Если хотя бы один бро­сок на 60 очков за­ме­нить брос­ком на 54 очка или мень­ше, то сумма умень­шит­ся как ми­ни­мум на 6, а, зна­чит, ста­нет не боль­ше 354 очков, что мень­ше 356 очков. Сле­до­ва­тель­но, бро­сок на 60 очков можно за­ме­нять толь­ко брос­ком на 57 очков. Но одна такая за­ме­на дает ито­го­вый ре­зуль­тат 357 очков, а хотя бы две за­ме­ны ― не более 354 очков. Зна­чит, 356 очков ше­стью брос­ка­ми на­брать не­воз­мож­но.
в) Как было по­ка­за­но в пунк­те б) каж­дый бро­сок при­но­сит иг­ро­ку не более 60 очков. Зна­чит, за 16 брос­ков он на­бе­рет не более 960 очков, а тогда для того, чтобы на­брать 1001 очко по­на­до­бит­ся не менее 17 брос­ков.
По­ка­жем, что игрок может на­брать 1001 очко за 17 брос­ков. Пред­по­ло­жим, что он сде­лал 15 брос­ков на 60 очков (итого 900), один бро­сок в зону утро­е­ния сек­то­ра 17 (51 очко) и один бро­сок в цен­траль­ный сек­тор 50 очков. Тогда в сумме он на­бе­рет 900 + 51 + 50 = 1001 очко.
От­ме­тим, что в пунк­тах а) и в) уча­щий­ся мог при­ве­сти дру­гие вер­ные при­ме­ры.
Ответ: а) да; б) нет; в) за 17 брос­ков.

 

Най­ди­те все трой­ки на­ту­раль­ных чисел k, m и n, удо­вле­тво­ря­ю­щие урав­не­нию 

Ре­ше­ние.
1. Так как  то  и 
2. Пусть  тогда  от­ку­да  и 
3. Пусть  тогда  от­ку­да  и 
4. Далее ко­неч­ным пе­ре­бо­ром зна­че­ний  на­хо­дим все ре­ше­ния:

Ответ: